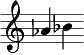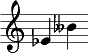In der Musiktheorie wird die Bezeichnung Intervall für die Tonhöhendifferenz zwischen zwei Tönen verwendet. Es handelt sich um harmonische Intervalle, wenn zwei Töne gleichzeitig erklingen und um melodische Intervalle, wenn sie nacheinander (sukzessive, aufwärts oder abwärts) erklingen.
Die Bezeichnungen der Intervalle bestehen aus zwei Teilen. Beispiele sind die »Große Terz« oder die »Reine Quinte«. In Walter Pistons »Harmony« werden die zwei Teile »spezifische Name« und »allgemeiner Name« genannt. Wikipedia spricht von »Intervallgruppen«, die die jeweiligen Bezeichnungen »klein«, »groß«, »vermindert« usw. zusammenfassen.
Sie können den allgemeinen Namen herausfinden, indem Sie die Ganztonschritte zählen. Wenn sich also das Intervall von E bis Gis erstreckt, zählen Sie von E bis G und erhalten den allgemeinen Namen Terz.

Die Intervallgruppe bezeichnet die exakte Größe des Intervalls. Primen, Quarten, Quinten und Oktaven können vermindert, rein oder übermäßig sein. Sekunden, Terzen, Sexten und Septimen können klein, groß, vermindert oder übermäßig sein. Ein kleines Intervall ist um einen Halbton kleiner als ein großes Intervall. Ein vermindertes Intervall ist um einen Halbton kleiner als ein reines oder kleines Intervall, und ein übermäßiges Intervall ist um einen Halbton größer als ein reines oder großes Intervall.
Versetzungszeichen ändern die Größe von Intervallen. Das Intervall wird einen Halbton größer, wenn Sie ein Kreuz vor den höchsten Ton setzen, oder um einen Halbton tiefer, wenn Sie ein b vor den tiefsten Ton setzen. Außerdem wird das Intervall einen Halbton kleiner mit einem d vor dem höchsten Ton oder einem Kreuz vor dem tiefsten Ton. In den folgenden Abschnitten wird die Benennung von Intervallen detailliert beschrieben.
Sekunden sind einfach erkennbar: Es sind die benachbarten Noten in der Notation. Eine der Noten ist auf einer Notenlinie, während die zweite sich im Zwischenraum darunter oder darüber befindet. Eine kleine Sekunde umfasst einen Halbtonschritt. Eine große Sekunde entspricht zwei Halbtonschritten, also einem Ganzton.
Um Sekunden richtig identifizieren zu können, sollten Sie zunächst lernen, welche Sekunden zwischen den Tönen der Durtonleiter liegen. Wie Sie in Abbildung 3.1 sehen können, sind nur die Intervalle E-F und B-C kleine Sekunden. Die Übrigen sind große Sekunden. Mit einem Klavier lässt sich verdeutlichen, dass Abbildung 3.1 korrekt ist. Es gibt nämlich keine schwarzen Tasten zwischen E und F und zwischen B und C.
Bei einer Sekunde mit Versetzungszeichen müssen wir herausfinden, wie sich diese auf die Größe des Intervalls auswirken. Lassen Sie uns nun einige Intervalle identifizieren.
Wir entfernen das Versetzungszeichen von dem Intervall in Abbildung 3.2 und stellen fest, dass es sich bei dem Intervall F-G um eine große Sekunde handelt. Wenn wir ein b zum höchsten Ton hinzufügen, wird das Intervall um einen Halbtonschritt kleiner und daher zu einer kleinen Sekunde.
Wir entfernen die Versetzungszeichen und sehen nun, dass das Intervall A-B eine große Sekunde ist. Erinnern Sie sich noch an Abbildung 3.1? Dann fügen wir das b zum A hinzu, wodurch das Intervall zur übermäßigen Sekunde wird. Wenn wir hingegen das b zum B hinzufügen, wird das Intervall zur großen Sekunde.
Wir entfernen die Versetzungszeichen und sehen nun, dass das Intervall E-F eine kleine Sekunde ist. Wenn wir das b zum tiefsten Ton hinzufügen, wird das Intervall einen Halbton größer und wird damit zur großen Sekunde. Wenn wir das Kreuz zum höchsten Ton hinzufügen, wird das Intervall einen Halbton größer und wird zur übermäßigen Sekunde.
Eine kleine Terz besteht aus einer kleinen und einer großen Sekunde oder drei Halbtonschritten. Eine große Terz entspricht zwei großen Sekunden oder vier Halbtonschritten. Abbildung 3.5 zeigt die Terzen zwischen allen natürlichen Tönen. Beachten Sie die großen Intervalle C-E, F-A und G-B. Dann sollten Sie wissen, dass die anderen vier Intervalle klein sind.
Dann untersuchen Sie die Versetzungszeichen, um zu sehen, ob sie den spezifischen Namen ändern. Dies geschieht auf die gleiche Weise wie bei Sekunden.
Eine reine Quarte entspricht 2½ Schritten oder zwei großen Sekunden und einer kleinen Sekunde. Abbildung 3.6 zeigt alle Quarten zwischen den natürlichen Tönen. Beachten Sie, dass die Quarte F-B übermäßig ist, während die anderen sechs rein sind.
Eine reine Quinte entspricht 3½ Schritten oder drei großen Sekunden und einer kleinen Sekunde. Abbildung 3.7 zeigt alle Quinten zwischen den natürlichen Tönen. Beachten Sie, dass alle Intervalle rein sind, während B-F vermindert ist.
If an interval has accidentals, then we must examine them to see how they change the size of the interval. A diminished fifth is one semitone smaller than a pure interval, and an augmented fifth is one semitone larger. Below you will find a few examples:
We remember from Abbildung 3.7 that the interval B-F is a diminished fifth. The lowest tone in Abbildung 3.8 is preceded by a flat that makes the interval one semitone larger and changes the interval from a diminished to a pure fifth.
We know from Abbildung 3.7 that interval E-B is a perfect fifth. In Abbildung 3.9 the E has a flat in front of it, making the interval augmented. But then the B is preceded by a double flat that makes the interval two semitone steps smaller and changes the interval to a diminished fifth.
Sixths are easiest identified by inverting the interval and identifying the third. Then the following rule applies:
Wenn die Terz vermindert ist, dann ist die Sexte übermäßig
Wenn die Terz klein ist, dann ist die Sexte groß
Wenn die Terz groß ist, dann ist die Sexte klein
Wenn die Terz übermäßig ist, dann ist die Sexte vermindert
If you find inverting intervals difficult, then you can memorise that the intervals E-C, A-F and B-G are minor. The other four are major. Then you examine the accidentals to see if they change the specific name. This is done exactly the same way as for seconds.
Septimen werden auf die gleiche Weise identifiziert wie Sexten. Wenn Sie eine Septime umkehren, erhalten Sie eine Sekunde.
If you find inverting intervals difficult, then you can memorise that the intervals C-B and F-E are major. The other five are minor. Then you examine the accidentals to see if they change the specific name. This is done exactly the same way as for seconds.