2.3 Elektronische Grundlagen
Die bisher in diesem Kapitel besprochenen mathematischen und logischen Funktionen werden in einem realen Computer durch elektronische Schaltungen realisiert. Das Kernstück von Logikschaltkreisen ist naturgemäß irgendeine Art von Schalter, der aber nicht von einem Menschen betätigt wird, sondern durch einen Steuerstrom. Wie im vorigen Kapitel dargelegt, wurden dazu in der Frühzeit der Computergeschichte elektromagnetische Relais verwendet, später Elektronenröhren und schließlich Transistoren. Auch bei modernen integrierten Schaltkreisen handelt es sich um Transistortechnik, die einfach nur auf Mikrometergröße verkleinert wurde. Ein moderner Mikroprozessor besteht aus Hunderten Millionen Transistoren.
Wie ebenfalls bereits erwähnt, heißt das Fachgebiet der Informatik, zu dem der Umgang mit elektronischen Schaltungen gehört, technische Informatik. Da es sich um die technische Umsetzung der booleschen Algebra handelt, wird sie auch als Schaltalgebra bezeichnet.
2.3.1 Einfache Schaltungen
Die grundlegenden Funktionen, die im Computer stattfinden, lassen sich sehr leicht als elektrische Schaltpläne darstellen. Die beiden einfachsten Schaltungen, die man sich vorstellen kann und die sich beispielhaft durch einfaches Elektrozubehör realisieren lassen, sind die Und- sowie die Oder-Schaltung: Um diese Elemente isoliert (ohne vollständigen Rechner) zu bauen, benötigen Sie lediglich eine Batterie, eine Glühlampe, zwei Schalter und etwas Draht.
Die Und-Schaltung lässt sich durch Reihenschaltung der beiden Schalter realisieren. Die Schalter entsprechen dabei den beiden Werten, die miteinander verknüpft werden sollen. Ein geöffneter Schalter steht für 0, ein geschlossener bedeutet 1. Die Lampe zeigt das Ergebnis an: Bei einer Reihenschaltung leuchtet sie natürlich nur dann, wenn beide Schalter geschlossen sind. Abbildung 2.3 zeigt den Aufbau dieser Schaltung.
Abbildung 2.3 Logisches Und durch einfache Schalter
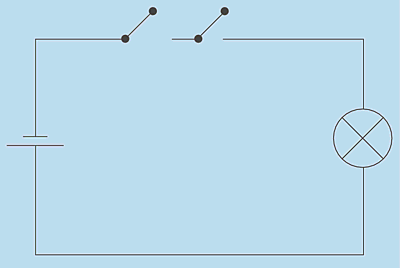
Wenn Sie die beiden Schalter dagegen parallel zueinander setzen, erhalten Sie eine Oder-Schaltung: Es genügt, dass einer der beiden Schalter geschlossen ist, um die Lampe zum Leuchten zu bringen (siehe Abbildung 2.4).
Abbildung 2.4 Logisches Oder durch einfache Schalter
In der Praxis werden die Schalter natürlich durch Transistoren ersetzt; statt der Glühlampe führt der Ausgang einer solchen Schaltung zur nächsten, um auf diese Weise komplexere logische Schaltkreise zu realisieren.
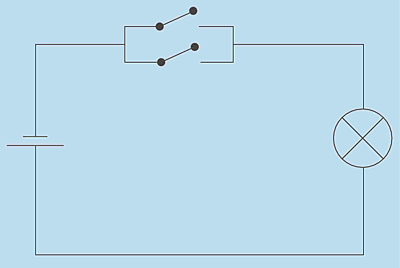
Ein MOS-Transistor (Metal Oxide Semiconductor oder deutsch: Metalloxidhalbleiter) besitzt drei Anschlüsse: einen Stromeingang (Emitter oder source), einen Stromausgang (Kollektor oder drain) und einen Steuerungseingang (gate). Es fließt nur Strom zwischen Emitter und Kollektor, wenn eine Steuerspannung anliegt, sodass sich der Transistor als Schalter betrachten lässt, der durch eine Steuerspannung ein- und ausgeschaltet wird. Eine sinnvolle Anwendung ist die NOT-Schaltung, die den Eingangswert verneint. Sie wird realisiert, indem der Transistor mit einem Widerstand gekoppelt wird, wie in Abbildung 2.5 gezeigt.
Abbildung 2.5 NOT-Schaltung durch Transistor und Widerstand
Die einfachsten Schaltungen, die sich jeweils mithilfe von zwei Transistoren und einem
Widerstand realisieren lassen, sind die NAND- und die NOR-Schaltung. Es handelt sich um die Umkehrungen der Und- beziehungsweise Oder-Schaltungen:
NAND (Not AND) realisiert die Schaltfunktion  (A
(A  B) oder
B) oder  A
A 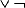 B, bei der die folgende Wertetabelle entsteht:
B, bei der die folgende Wertetabelle entsteht:
| NAND | 0 | 1 |
| 0 |
1 |
1 |
| 1 |
1 |
0 |
NOR (Not OR) stellt dagegen die Schaltfunktion  (A
(A  B) beziehungsweise
B) beziehungsweise  A
A 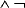 B dar, für die die folgende Wertebelegung gilt:
B dar, für die die folgende Wertebelegung gilt:
| NOR | 0 | 1 |
| 0 |
1 |
0 |
| 1 |
0 |
0 |
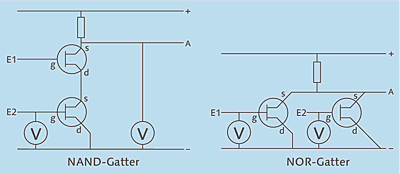
Abbildung 2.6 zeigt, wie die NAND- und die NOR-Schaltung durch zwei Transistoren und einen Widerstand realisiert werden.
Abbildung 2.6 NAND- und NOR-Schaltung durch je zwei Transistoren und einen Widerstand
Durch Kombination mit der zuvor gezeigten NOT-Schaltung lassen sich diese Schaltungen zu den bekannten AND- und OR-Funktionen ausbauen.
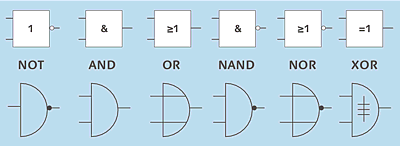
Für die bisher dargestellten Schaltungen gelten die vereinfachenden Symbole in Abbildung 2.7, weil sich auf diese Weise komplexere Gefüge aus solchen Schaltungen übersichtlich darstellen lassen. In diesem Zusammenhang werden die grundlegenden Schaltungen wie AND und OR als Gatter (Gates) bezeichnet.
Abbildung 2.7 Gattersymbole der Logikschaltungen – oben die aktuelle DIN-Norm, unten die traditionellen Symbole
Die Negation eines Wertes wird übrigens in der Regel nicht durch ein vollständiges NOT-Symbol dargestellt, sondern durch den kleinen Kreis, der auch bei den Symbolen für NAND und NOR zu finden ist. Genau wie bei diesen Schaltungen der Ausgang negiert wird, wird bei anderen ein Eingang negiert, das heißt, ein NOT-Gatter wird vor einen der beiden Eingänge eines anderen Elements gesetzt. Beachten Sie, dass die tatsächliche technische Realisation von Schaltungen nicht mit der schematischen Darstellung übereinstimmen muss. Wie Sie zuvor gesehen haben, werden beispielsweise nicht etwa NAND und NOR durch Verneinung von AND und OR gebaut, sondern in Wirklichkeit ist es gerade umgekehrt. Im Übrigen gibt es für komplexere Verknüpfungen von Schaltungen oft eine Reihe äquivalenter Lösungen.
Die XOR-Schaltung (Exklusiv-Oder), die beispielsweise für den im Folgenden besprochenen
Halbaddierer benötigt wird, ist ein wenig komplexer zu realisieren. Sie besteht beispielsweise
aus zwei AND-Gattern mit je einem negierten Eingang, auf die dieselben eingehenden
Spannungen verteilt werden. Die Ausgänge der beiden AND-Gatter werden wiederum durch
ein OR-Gatter verknüpft. Wie Sie sehen, entspricht diese Beschreibung dem zuvor erwähnten
Ausdruck ( A
A  B)
B)  (A
(A 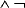 B).
B).
2.3.2 Zusammengesetzte Schaltungen
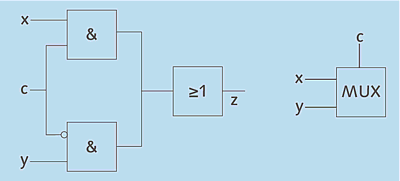
Ein Beispiel für die Verknüpfung mehrerer einfacher Gatter ist der Multiplexer. Er implementiert eine einfache Wenn-dann-Beziehung: Wenn der Steuereingang c mit einer Spannung belegt ist (Wert 1), wird der Wert des Eingangs x durchgeschaltet, andernfalls der Wert des Eingangs y. Abbildung 2.8 zeigt den schematischen Aufbau des Multiplexers, daneben sein Schaltsymbol. Die schrittweise Zusammenfassung immer komplexerer Schaltungen durch neue Symbole ist eine wichtige Voraussetzung für die effiziente Arbeit bei der Entwicklung elektronischer Bauteile.
Abbildung 2.8 Aufbau eines Multiplexers
Ein weiteres interessantes Bauteil ist der Halbaddierer. Dieser Name leitet sich aus der Tatsache her, dass die Schaltung zwar einen Übertrag
berechnet, wenn beide Eingangswerte 1 sind, aber nicht in der Lage ist, den Übertrag
eines vorgeschalteten Addierers entgegenzunehmen. Diese Fähigkeit besitzt nur der
komplexere, im Folgenden dargestellte Volladdierer. Beim Halbaddierer werden die Werte der beiden Eingänge x und y addiert. Der Ausgang
s (»sum«, also Summe) liefert das einstellige Ergebnis der Addition, das der Verknüpfung
x XOR y entspricht, während c (»carry«, der Übertrag) den Wert 1 für die nächste Stelle
liefert, wenn x und y beide 1 sind. Die Funktion, die zum Ergebnis von c führt, ist
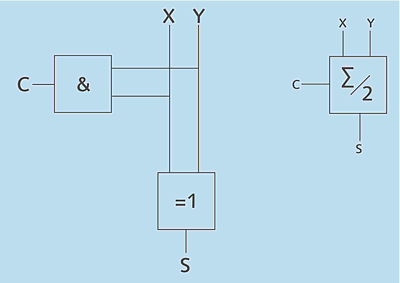
demzufolge x  y. Abbildung 2.9 zeigt den Aufbau des Halbaddierers und sein Schaltsymbol.
y. Abbildung 2.9 zeigt den Aufbau des Halbaddierers und sein Schaltsymbol.
Abbildung 2.9 Aufbau eines Halbaddierers
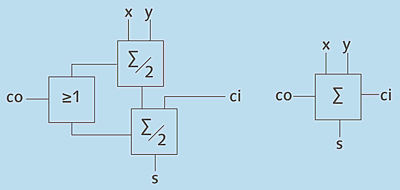
Der Volladdierer enthält zwei Halbaddierer. Die einstellige Summe setzt sich aus der Summe der beiden eigentlichen Summanden x und y und aus dem hereinkommenden Übertrag ci (Carry-in) zusammen. Der ausgehende Übertrag co (Carry-out) wird durch die Oder-Verknüpfung der beiden Summen gebildet. In Abbildung 2.10 sehen Sie den Aufbau des Volladdierers und sein Schaltsymbol.
Abbildung 2.10 Aufbau eines Volladdierers
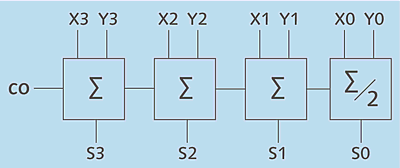
Aus einer Reihe dieser 1-Bit-Volladdierer lässt sich ein n-Bit-Addierwerk realisieren. Der Übertrag eines dieser Addierer wird dabei jeweils in den nächsten übertragen. Beachten Sie, dass der Baustein ganz rechts ein Halbaddierer ist, weil die kleinste Stelle natürlich kein Carry-in zu verarbeiten hat. Wenn Sie sämtliche s-Ausgänge von links nach rechts lesen, erhalten Sie das duale Rechenergebnis; ganz links kommt zusätzlich das Carry-out der höchsten Stelle heraus. In Abbildung 2.11 sehen Sie beispielsweise einen 4-Bit-Addierer, mit dem sich zwei Werte von 0000 bis 1111 (0 bis 15) addieren lassen.
Abbildung 2.11 Aufbau eines 4-Bit-Addierwerks
Speicherbausteine
Die bisher untersuchten komplexen Schaltungen sind in der Lage, verschiedene Operationen durchzuführen. Eine andere Art von Bausteinen dient dagegen nicht als Rechenwerkzeug, sondern als Speicher, bei dem ein einmal gesetzter Wert dauerhaft vorgehalten wird. Erreicht wird dies durch verschiedene Arten der Rückkopplung: Ein Ausgang einer Schaltung wird mit einem Eingang verbunden, um einen einmal eingegebenen Wert immer wieder in die Schaltung zurückzuschreiben.
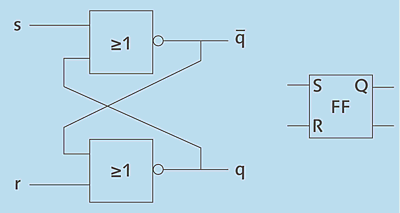
Der wichtigste Grundbaustein zur Realisierung von Speichern ist das Flip-Flop. Der Name dieses Bausteins beschreibt die beiden verschiedenen Zustände, die er einnehmen und dauerhaft halten kann. Die bekannteste Art des Flip-Flops ist das RS-Flip-Flop (für Set und Reset). Es handelt sich um zwei NOR-Gatter, die über je einen freien Eingang (r und s genannt) verfügen. Die beiden anderen Eingänge der NOR-Gatter werden mit den Ausgängen des jeweils anderen Gatters verbunden. In Abbildung 2.12 sehen Sie die Schaltzeichnung des RS-Flip-Flops sowie sein vereinfachtes Schaltsymbol zur weiteren Verwendung.
Abbildung 2.12 Aufbau eines RS-Flip-Flops
Der schaltlogisch interessante Ausgang des RS-Flip-Flops ist q: Wenn über s (Set) auch nur kurzzeitig der Wert 1 übergeben wird, liefert q diese 1 dauerhaft. Wird dagegen r (Reset) mit einer 1 belegt, dann wird q zurückgesetzt und liefert auf Dauer eine 0. Auf diese Weise dient das RS-Flip-Flop als wichtigste Komponente von Speicherbausteinen; es handelt sich um einen 1-Bit-Speicher.
Um vollständige Speicherbausteine zu realisieren, müssen außerhalb des RS-Flip-Flops noch einige weitere Schaltelemente hinzugefügt werden, die dazu dienen, den Eingabewert aus einer einzelnen Leitung als Wert zu interpretieren, der in der Speicherzelle abgelegt werden soll. Dazu muss ein Schalter verwendet werden, der bestimmt, dass das aktuelle Signal des Eingangs im RS-Flip-Flop gespeichert werden soll. Außerdem muss je nach zu speicherndem Wert zwischen dem Eingang s und dem Eingang r gewählt werden: Eine 1 kann einfach an die Leitung s durchgeschaltet werden, eine 0 bedeutet dagegen, dass eine 1 auf r eingegeben werden soll – der Wert muss nach Auswahl von r zusätzlich negiert werden.
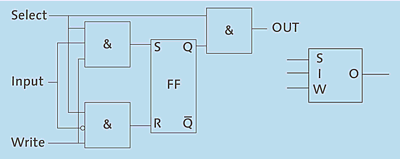
Abbildung 2.13 zeigt den Aufbau einer Speicherzelle, die die beschriebene Funktionalität zur Verfügung stellt, sowie ihr Schaltsymbol. Wenn auf SELECT eine 1 eingegeben wird, kann über den mit Q AND-verknüpften Ausgang OUT der aktuelle Wert gelesen werden. Dieser Mechanismus dient in einem großen Gefüge von Speicherzellen der Adressierung, also der Auswahl einer bestimmten Speicherzelle oder einer Gruppe von Speicherzellen. Werden SELECT = 1 und WRITE = 1 gesetzt, wird der an INPUT anliegende Wert auf die beschriebene Weise im Flip-Flop abgelegt.
Abbildung 2.13 Aufbau einer Speicherzelle
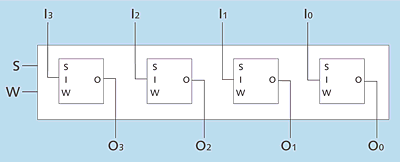
Mehrere Speicherzellen lassen sich zu einem Register zusammenschließen. Dazu werden die SELECT- und WRITE-Eingänge aller beteiligten Zellen zusammengeschlossen, da stets das gesamte Register auf einmal gelesen oder geschrieben wird. Auf diese Weise werden die Rechenregister im Mikroprozessor realisiert, aber auch die adressierbaren Speicherblöcke im Arbeitsspeicher (RAM). Abbildung 2.14 zeigt ein Beispiel eines 4-Bit-Registers. In der Praxis sind die meisten heutigen Register 32 oder gar 64 Bit breit, funktionieren aber nach demselben Prinzip.
Abbildung 2.14 Aufbau eines 4-Bit-Registers
Ihr Kommentar
Wie hat Ihnen das <openbook> gefallen? Wir freuen uns immer über Ihre freundlichen und kritischen Rückmeldungen.



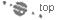

 Jetzt bestellen
Jetzt bestellen






