2 Mathematische und technische Grundlagen
Unser Dasein liegt zwischen zwei Ewigkeiten.
– Blaise Pascal
Dieses Kapitel bildet die Grundlage für das Verständnis von Computerprogrammen. Wer die Logik versteht, die den einzelnen Vorgängen in Computersystemen zugrunde liegt, wird geringere Schwierigkeiten haben, mit Software umzugehen. Die konkrete Verwirklichung maßgeblicher logischer Funktionen durch elektronische Bauteile wird hier ebenfalls behandelt. Das Kapitel wird durch eine einfache Prozessorsimulation abgerundet, die sowohl auf dem Papier als auch als Programm auf einem gewöhnlichen PC mit einer einfachen Sprache programmiert werden kann.
Die grundlegenden Arbeitsschritte, die ein Computer ausführt, sind mathematische und logische Operationen: Der Mikroprozessor verknüpft Werte, die ihm ein Programm übergibt oder die er auf Anweisung aus dem Speicher oder von einem Eingabegerät liest, nach verschiedenen Vorschriften. Dazu gehören Grundrechenarten, Vergleiche und Wenn-dann-Beziehungen.
2.1 Einführung in die Logik
Der Begriff Logik ist von dem griechischen Wort 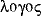 (logos) abgeleitet. Die Bedeutung dieses Wortes hat eine lange Geschichte und ist nicht
ganz eindeutig. Die Wurzel des Wortes stammt von dem altgriechischen Verb
(logos) abgeleitet. Die Bedeutung dieses Wortes hat eine lange Geschichte und ist nicht
ganz eindeutig. Die Wurzel des Wortes stammt von dem altgriechischen Verb 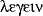 (legéin), das zunächst für »sammeln« oder »auflesen« steht; es ist verwandt mit lateinisch
»legere« und deutsch »lesen«.
(legéin), das zunächst für »sammeln« oder »auflesen« steht; es ist verwandt mit lateinisch
»legere« und deutsch »lesen«.
Aus der Sicht der Informatik ist die wichtigste Form der Logik die formale Logik. Ihre klassische Form ist die Aussagenlogik, die Wissenschaft von der Verknüpfung und Wechselwirkung von Aussagen. Eine Aussage ist dabei ein beliebiger Satz, der eindeutig wahr oder eindeutig falsch ist, dessen Wahrheit also überprüft werden kann. Für die Mathematik wurde die Aussagenlogik
erst nutzbar, als Gottlob Frege 1879 die Prädikatenlogik entwickelte, eine mathematisch-formale Schreibweise für Aussagen, auf der einige
der im Folgenden verwendeten mathematischen Sätze basieren. Typische Formulierungen
der Prädikatenlogik sind die bekannten Satzanfänge »Für alle x gilt: ...« (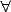 x) oder »Es gibt (mindestens) ein x, für das gilt: ...« (
x) oder »Es gibt (mindestens) ein x, für das gilt: ...« (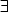 x).
x).
2.1.1 Aussagen
Aussagen sind beispielsweise die folgenden Sätze:
- »Der Kölner Dom ist 157 Meter hoch.«
- »Der Kölner Dom ist 17 Meter hoch.«
- »Ich bin 17 Meter groß.«
Die folgenden Sätze sind dagegen aus verschiedenen Gründen keine Aussagen:
- »Der Kölner Dom ist schön.« – dies ist eine subjektive Meinungsäußerung, die für den einen wahr und für den anderen falsch sein kann.
- »Ist heute Freitag?« – eine Frage ist keine Aussage; in diesem Fall kann die Antwort eine Aussage sein.
- »Wie geht es dir?« – ebenfalls eine Frage, allerdings ist hier auch die Antwort keinesfalls eine Aussage (sie ergibt wieder eine subjektive Meinungsäußerung).
Die Art von Aussagen, die im Zusammenhang mit Informatik und Computern besonders interessant ist, sind die mathematischen Aussagen. Eine mathematische Aussage ist ein System, das aus Termen (mathematischen Ausdrücken) besteht. Ein Term ist im einfachsten Fall eine numerische Konstante wie beispielsweise 100 oder –3,25, in komplexeren Fällen eine arithmetische Verknüpfung wie etwa 3 + 5, die sich in einen konkreten Wert auflösen lassen muss. Eine vollständige mathematische Aussage ist ein Vergleich zwischen Termen, der zwei mögliche Formen annehmen kann:
- Die Gleichung ist eine wahre Aussage, wenn die beiden verknüpften Terme den gleichen Wert haben.
- Die Ungleichung ist dagegen dann eine wahre Aussage, wenn die Werte der beiden verknüpften Terme auf eine vorgegebene Weise unterschiedlich sind.
Beispiele für mathematische Aussagen sind folgende:
- 5 + 6 = 6 + 5 ist eine Gleichung.
- 5 + 6 < 6 + 5 ist eine Ungleichung; die Beziehung lautet in diesem Fall »ist kleiner als«.
Sowohl sprachliche als auch mathematische Aussagen können, wie bereits erwähnt, wahr oder falsch sein. Hier sehen Sie einige Beispiele für wahre und falsche Aussagen:
- »Der Kölner Dom ist 17 Meter hoch.« – falsche sprachliche Aussage
- »Ein Tag hat 24 Stunden.« – wahre sprachliche Aussage
- 5 > 7 – falsche mathematische Aussage (Ungleichung)
- 7 > 5 – wahre mathematische Aussage (Ungleichung)
- 3 + 4 = 34 – falsche mathematische Aussage (Gleichung)
- 3 + 4 = 7 – wahre mathematische Aussage (Gleichung)
2.1.2 Aussageformen
Die in der Mathematik weitverbreiteten Formeln und verallgemeinerten Gleichungen mit Platzhaltern (Variablen oder Unbekannten) sind keine Aussagen. Schließlich gilt für sie die Bedingung nicht, dass sie eindeutig wahr oder falsch sein müssen. Beispielsweise lässt sich die allgemeine Gleichung a + b = 3 mit unendlich vielen Werten zu einer wahren oder auch zu einer falschen Aussage machen:
- a = 2; b = 1 oder a = 3,5; b = –0,5 ergeben eine wahre Aussage.
- a = 3; b = 5 oder a = 0,75; b = 0,2 ergeben eine falsche Aussage.
Ein Wert, der in eine Aussageform eingesetzt wird und diese zu einer wahren Aussage macht, wird als Lösung dieser Aussageform oder genauer als Teil ihrer Lösungsmenge bezeichnet.
Das folgende Beispiel zeigt, wie die Lösungsmenge einer linearen Gleichung mit einer Unbekannten bestimmt wird:
2x + 7 = 21 | –7
2x = 14 | :2
x = 7
Lineare Gleichungen besitzen in der Regel genau eine Lösung. Komplexere Gleichungssysteme können dagegen auch Lösungsmengen besitzen, die aus keiner, aus mehreren oder aus unendlich vielen Lösungen bestehen.
Das Lösen von Ungleichungen ist der Versuch, eine Menge von Werten zu bestimmen, die in die Aussageform einer Ungleichung eingesetzt werden können, um eine wahre Aussage zu erhalten:
2x + 7 < 21 | –7
2x < 14 | :2
x < 7
Die Lösungsmenge der Ungleichung ist die Menge aller x, für die gilt, dass x kleiner als 7 ist. Mathematisch wird dies folgendermaßen ausgedrückt:
L = {x | x < 7}
2.1.3 Logische Verknüpfungen
Nicht immer werden nur einzelne Aussagen betrachtet. Es ist üblich und oft notwendig, mehrere Aussagen mithilfe verschiedener logischer Verknüpfungen zu verbinden. Dazu gehören sowohl logische Schlussfolgerungen (Wenn-dann-Beziehungen) als auch einfache Und- sowie Oder-Verknüpfungen.
Das gesamte Fachgebiet der logischen Verknüpfungen wird auch als boolesche Algebra bezeichnet, benannt nach dem britischen Mathematiker George Boole, der bereits im 19. Jahrhundert eine Algebra der binären logischen Verknüpfungen entwickelte.
Logische Schlussfolgerungen
Die Schlussfolgerung, das Lieblingsspielzeug der philosophischen Logik, ist eine Wenn-dann-Beziehung zwischen Aussagen; sie wird auch als Implikation bezeichnet. Auch Computerprogramme arbeiten mit dieser Art der Logik, weil sie oft anhand bestimmter Bedingungen Entscheidungen treffen müssen.
In der sprachlichen Aussagenlogik sieht eine Schlussfolgerung beispielsweise folgendermaßen aus:
- Es regnet.
- Die Straße wird nass.
Schlussfolgerung: Wenn es regnet, wird die Straße nass.
Oder in formaler Schreibweise: Es regnet.  Die Straße wird nass.
Die Straße wird nass.
Das Zeichen  wird als »daraus folgt« aufgelöst.
wird als »daraus folgt« aufgelöst.
Die direkte Umkehrung einer solchen Schlussfolgerung ist nicht automatisch zulässig: Eine Aussage wie
A  B (aus A folgt B)
B (aus A folgt B)
bedingt nicht den folgenden Schluss:
B  A (aus B folgt A)
A (aus B folgt A)
Sprachlich formuliert gilt also nicht die folgende Schlussfolgerung: Wenn die Straße nass wird, regnet es. Schließlich kann es zahlreiche Gründe dafür geben, warum eine Straße nass wird.
Den korrekten, zulässigen Umkehrschluss bildet dagegen die verneinte Umkehrung:
 B
B 
 A (aus Nicht-B folgt Nicht-A)
A (aus Nicht-B folgt Nicht-A)
Auf das Sprachbeispiel übertragen: Wenn die Straße nicht nass wird, dann regnet es nicht. Dieser Satz ist intuitiv einleuchtend und richtig.
Zur Verdeutlichung sehen Sie hier alle erlaubten Umkehrschlüsse im Überblick:
- A
 B; Umkehrung:
B; Umkehrung:  B
B 
 A
A
Beispiel: Wenn es regnet, wird die Straße nass.
Umkehrung: Wenn die Straße nicht nass wird, dann regnet es nicht. - A

 B; Umkehrung: B
B; Umkehrung: B 
 A
A
Beispiel: Wenn die Sonne scheint, ist es nicht Nacht.
Umkehrung: Wenn es Nacht ist, scheint nicht die Sonne.[Anm.: Natürlich gibt es Gegenden auf der Welt, wo dieser Bezug nicht zutrifft. Wie bei den meisten Aussagen gibt es Nebenbedingungen, die stillschweigend gelten – hier beispielsweise: »Wenn die Sonne außerhalb des Polarsommers scheint, dann ist nicht Nacht.«]  A
A  B; Umkehrung:
B; Umkehrung:  B
B  A
A
Beispiel: Wenn nicht Wochenende, Feiertag oder Urlaub ist, dann muss ich arbeiten. Umkehrung: Wenn ich nicht arbeiten muss, dann ist Wochenende, Feiertag oder Urlaub.
 A
A 
 B; Umkehrung: B
B; Umkehrung: B  A
A
Beispiel: Wenn ich nicht den Führerschein habe, darf ich nicht Auto fahren. Umkehrung: Wenn ich Auto fahren darf, habe ich den Führerschein.
Und- und Oder-Verknüpfungen
Die beiden Verknüpfungen Und und Oder (AND und OR) sind die wichtigsten Mittel zur Verbindung mehrerer Aussagen oder Bedingungen. Werden
mehrere Aussagen durch Und ( ) verknüpft (Konjunktion), ergibt sich nur dann eine wahre Aussage, wenn alle Teilaussagen wahr sind.
) verknüpft (Konjunktion), ergibt sich nur dann eine wahre Aussage, wenn alle Teilaussagen wahr sind.
Die Verknüpfung A  B ist also nur dann wahr, wenn sowohl A als auch B wahre Aussagen sind.
B ist also nur dann wahr, wenn sowohl A als auch B wahre Aussagen sind.
Sprachlich kann dies sehr gut durch zusammengesetzte Wenn-Bedingungen bei der Schlussfolgerung gezeigt werden. Zum Beispiel:
Wenn die Glühbirne funktioniert und der Lichtschalter eingeschaltet wird, dann leuchtet das Licht.
Oder als einzelne Aussagen:
- Die Glühbirne funktioniert.
- Der Lichtschalter ist eingeschaltet.
- Das Licht leuchtet.
Die erste und die zweite Aussage werden hier durch Und verknüpft und ergeben so die dritte Aussage:
Die Glühbirne funktioniert.  Der Lichtschalter ist eingeschaltet.
Der Lichtschalter ist eingeschaltet.  Das Licht leuchtet.
Das Licht leuchtet.
Schematisch lassen sich solche Verknüpfungen am einfachsten durch eine sogenannte
Wahrheitswertetabelle darstellen. In einer solchen Tabelle (wie übrigens auch bei den Abläufen innerhalb
eines Computers) wird eine wahre Aussage durch den Wert 1 und eine falsche Aussage
durch die 0 dargestellt. Die Wahrheitswertetabelle für Und ( ) sieht also folgendermaßen aus:
) sieht also folgendermaßen aus:

|
0 | 1 |
| 0 |
0 |
0 |
| 1 |
0 |
1 |
Logische Operationen wie die Und-Verknüpfung können im Computer auf zweierlei Arten genutzt werden:
- Die logische Und-Operation dient tatsächlich, wie zuvor dargestellt, der Verkettung verschiedener Bedingungsprüfungen: Ein Programm soll einen bestimmten Schritt nur dann ausführen, wenn mehrere Teilbedingungen zutreffen.
- Demgegenüber verknüpft die bitweise Und-Operation die einzelnen Bits gespeicherter Werte, bevorzugt ganzer Zahlen. Dies wird beispielsweise genutzt, um aus einer Teilnetzmaske und einer IP-Adresse die Adresse des Netzwerks zu ermitteln (siehe Kapitel 4, »Netzwerkgrundlagen«).
In der Programmiersprache C und allen Sprachen, die ihre grundlegende Syntax erben, wird das logische Und beispielsweise durch && dargestellt, bitweises Und dagegen durch &. Einzelheiten zur Verwendung bei der Programmierung erfahren Sie in Kapitel 9, »Grundlagen der Programmierung«.
Eine Und-Verknüpfung sowie wie die im Anschluss dargestellte Oder-Verknüpfung lassen sich hardwaretechnisch durch recht simple Schaltungen realisieren. Genaues erfahren Sie in Abschnitt 2.3.1, »Einfache Schaltungen«.
Werden dagegen mehrere Aussagen durch Oder ( ) verknüpft (Disjunktion), dann ist die Gesamtaussage wahr, wenn mindestens eine der Teilaussagen zutrifft.
) verknüpft (Disjunktion), dann ist die Gesamtaussage wahr, wenn mindestens eine der Teilaussagen zutrifft.
Die Beziehung A  B ist also wahr, wenn A wahr ist, falls B wahr ist oder auch, wenn A und B wahr sind.
Hier sehen Sie zunächst wieder ein sprachliches Beispiel:
B ist also wahr, wenn A wahr ist, falls B wahr ist oder auch, wenn A und B wahr sind.
Hier sehen Sie zunächst wieder ein sprachliches Beispiel:
Wenn ich eine Million im Lotto oder bei einer Quiz-Sendung gewinne, dann bin ich Millionär. Die einzelnen Aussagen sind folgende:
- Ich gewinne eine Million im Lotto.
- Ich gewinne eine Million bei einer Quiz-Sendung.
- Ich bin Millionär.
Formal sieht diese Oder-Verknüpfung der beiden ersten Aussagen so aus:
Ich gewinne eine Million im Lotto.  Ich gewinne eine Million bei einer Quiz-Sendung.
Ich gewinne eine Million bei einer Quiz-Sendung.  Ich bin Millionär.
Ich bin Millionär.
Es ist egal, ob nur eine der beiden Voraussetzungen zutrifft oder ob beide wahr sind – in beiden Fällen stimmt die Schlussfolgerung.
Auch die Oder-Verknüpfung kann logisch oder bitweise eingesetzt werden; C und syntaktisch ähnliche Sprachen verwenden für das logische Oder die Zeichen ||, für das bitweise Oder dagegen |.
Hier wieder die entsprechende schematische Darstellung als Wahrheitswertetabelle.

|
0 | 1 |
| 0 |
0 |
1 |
| 1 |
1 |
1 |
Die folgende Tabelle zeigt eine Übersicht der Und- und Oder-Verknüpfungen aller vier möglichen logischen Belegungen zweier Wahrheitswerte A und B sowie all ihrer Verneinungen.
Aus den Verhältnissen in Tabelle 2.3 ergeben sich die beiden folgenden wichtigen Äquivalenzen, die nach dem schottischen Mathematiker Augustus De Morgan als De-Morgan-Theoreme bezeichnet werden:
 A
A 
 B
B 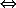
 (A
(A  B)
B)
 A
A 
 B
B 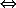
 (A
(A  B)
B)
Diese Beziehungen müssen Sie beim Programmieren beachten, wenn Sie verknüpfte Wenn-dann-Bedingungen formulieren.
Zu guter Letzt gibt es eine dritte wichtige logische Verknüpfung, die als Exklusiv-Oder bezeichnet wird. Da sie in der Mathematik nicht verwendet wird, besitzt sie kein traditionelles Zeichen, sondern wird in der Regel durch den abgekürzten englischen Namen XOR (eXclusive OR) bezeichnet.
Eine XOR-Verknüpfung zweier Aussagen ist nur dann wahr, wenn genau eine Teilaussage wahr ist. Es ist recht schwierig, ein anschauliches sprachliches Beispiel für diese Verknüpfung zu finden. Das XOR steht im Grunde für ein »Entweder-Oder«: Wenn ich entweder mit dem Bus oder mit dem Auto den richtigen Weg fahre, gelange ich zur Arbeit (ich kann auf keinen Fall mit Bus und Auto gleichzeitig fahren).
Tabelle 2.4 zeigt die möglichen Ergebnisse der XOR-Verknüpfung.
| XOR | 0 | 1 |
| 0 |
0 |
1 |
| 1 |
1 |
0 |
Viele Programmiersprachen besitzen keine eingebaute XOR-Operation. In diesen lässt sie sich durch den folgenden komplexeren Ausdruck simulieren:
A XOR B = ( A
A  B)
B)  (A
(A 
 B)
B)
In der Programmiersprache C gibt es XOR nur als Bit-Operator, nicht aber als logischen Operator. Das Symbol dafür ist ^. Das bitweise XOR wird insbesondere für Verschlüsselungs- und Prüfsummenoperationen eingesetzt, denn eine interessante Besonderheit der XOR-Operation besteht darin, dass ihre Umkehrung wieder eine XOR-Operation ist – es gilt:
A XOR B = C 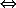 (C XOR A = B)
(C XOR A = B)  (C XOR B = A)
(C XOR B = A)
Eine wichtige Beispielanwendung ist die Berechnung der Prüfsumme (Parity) in bestimmten RAID-Arrays. Es handelt sich um eine Zusammenfassung mehrerer Festplatten, die einer Steigerung der Performance und/oder Datensicherheit insbesondere bei Serversystemen dienen (siehe Kapitel 3, »Hardware«). RAID 3, 4 und 5 verknüpfen dabei zwei oder mehr gleich lange Bitfolgen mit einer XOR-Operation. Wenn eine der beteiligten Festplatten versagt, lässt sich somit aus der umgekehrten XOR-Operation mit der intakten Folge beziehungsweise den intakten Folgen einerseits und der Prüfsumme andererseits die defekte Folge rekonstruieren.
Vergleichsoperationen
Diese Art logischer Verknüpfungen erzeugt Aussagen durch die Überprüfung von Termen auf Gleichheit oder Ungleichheit. Die resultierenden Aussagen können also wahr oder falsch sein.
- Gleichheit:
A = B (A gleich B) ist wahr, wenn A den gleichen Wert hat wie B.
- Ungleichheit:
A
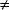 B (A ungleich B) ist wahr, wenn A einen anderen Wert hat als B.
B (A ungleich B) ist wahr, wenn A einen anderen Wert hat als B.
- Ungleichheit mit Richtungsangabe:
- A
 B (A ist kleiner als B) ist wahr, wenn A einen geringeren Wert hat als B.
B (A ist kleiner als B) ist wahr, wenn A einen geringeren Wert hat als B.
- A > B (A ist größer als B) ist wahr, wenn A einen höheren Wert hat als B.
- A
 B (A ist kleiner oder gleich B) ist wahr, wenn A entweder einen geringeren Wert als
B oder den gleichen Wert wie B hat.
B (A ist kleiner oder gleich B) ist wahr, wenn A entweder einen geringeren Wert als
B oder den gleichen Wert wie B hat.
- A
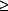 B (A ist größer oder gleich B) ist wahr, wenn A entweder einen höheren Wert als B
oder den gleichen Wert wie B hat.
B (A ist größer oder gleich B) ist wahr, wenn A entweder einen höheren Wert als B
oder den gleichen Wert wie B hat.
- A
A  B ist eine Kurzfassung für: A < B
B ist eine Kurzfassung für: A < B  A = B. A
A = B. A 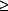 B ist entsprechend eine Kurzfassung für: A
B ist entsprechend eine Kurzfassung für: A  B
B  A = B.
A = B.
Die Umkehrungen (gegenteilige Aussagen) der Vergleichsoperationen sollten Sie sich merken:
- Die Umkehraussage von A = B ist A
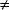 B.
B.
- A < B besitzt die Umkehraussage A
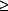 B.
B.
- A
 B hat schließlich die Umkehraussage A
B hat schließlich die Umkehraussage A  B.
B.
Tabelle 2.5 verdeutlicht dies an Beispielen für den Vergleich verschiedener ganzzahliger Werte. Beachten Sie, dass die verknüpften Werte ganze Zahlen, die Ergebnisse (1 oder 0) aber Wahrheitswerte sind.
| Verknüpfung | A=2, B=2 | A=2, B=3 | A=3, B=2 |
| A = B |
1 |
0 |
0 |
A 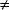 B B
|
0 |
1 |
1 |
A  B B
|
0 |
1 |
0 |
A  B B
|
0 |
0 |
1 |
A  B B
|
1 |
1 |
0 |
A 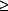 B B
|
1 |
0 |
1 |
Logische Verknüpfungen in Computerprogrammen
Da Zeichen wie 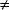 ,
,  oder
oder  nicht zum ASCII-Zeichensatz (dem ursprünglichen Standard-Computerzeichensatz) gehören,
haben sich die Entwickler der verschiedenen Programmiersprachen andere Zeichen beziehungsweise
Zeichenkombinationen ausgedacht. Ärgerlicherweise sind diese Bezeichnungen in den
verschiedenen Sprachen nicht einheitlich. Tabelle 2.6 zeigt die Schreibweisen der Programmiersprachen C und Pascal im Vergleich. Beachten
Sie, dass die C-Schreibweise in einer ganzen Reihe von Sprachen verwendet wird, beispielsweise
C++, Java, JavaScript, Perl, Ruby, PHP und so weiter. Die Pascal-Schreibweise nutzen
dagegen auch einige BASIC-Dialekte.
nicht zum ASCII-Zeichensatz (dem ursprünglichen Standard-Computerzeichensatz) gehören,
haben sich die Entwickler der verschiedenen Programmiersprachen andere Zeichen beziehungsweise
Zeichenkombinationen ausgedacht. Ärgerlicherweise sind diese Bezeichnungen in den
verschiedenen Sprachen nicht einheitlich. Tabelle 2.6 zeigt die Schreibweisen der Programmiersprachen C und Pascal im Vergleich. Beachten
Sie, dass die C-Schreibweise in einer ganzen Reihe von Sprachen verwendet wird, beispielsweise
C++, Java, JavaScript, Perl, Ruby, PHP und so weiter. Die Pascal-Schreibweise nutzen
dagegen auch einige BASIC-Dialekte.
Die in der Tabelle aufgeführte Wertzuweisung betrifft eine Besonderheit von Variablen in Programmiersprachen: Während eine Variable in der Mathematik lediglich ein Platzhalter ist, der für beliebige Werte stehen kann, ist sie in einer Programmiersprache ein Speicherplatz, der bei der Ausführung des Programms einen bestimmten, wohldefinierten Wert enthält. Die Wertzuweisungsoperation dient dazu, ihr einen solchen Wert zuzuteilen.
2.1.4 Mengenoperationen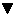
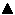
Eine spezielle Form der logischen Verknüpfung beschäftigt sich mit den Beziehungen zwischen einem einzelnen Element und einer Menge beziehungsweise zwischen zwei Mengen. Eine Menge ist eine Gruppe mehrerer Werte, die entweder als Abfolge einzelner Zahlen oder durch bestimmte Regeln definiert wird.
Beachten Sie für die Umsetzung im Computer, dass Mengenoperationen nicht in jeder Programmiersprache eingebaut sind. In Kapitel 10, »Konzepte der Programmierung«, werden allerdings einige Strategien vorgestellt, wie Sie Listen oder Mengen in verschiedenen Sprachen erzeugen und damit arbeiten.
Beziehungen zwischen Mengen und einzelnen Werten
Ein Wert ist Element einer Menge, wenn dieser Wert in der Menge vorkommt. Ein Wert ist nicht Element einer Menge, wenn dieser Wert nicht in der Menge vorkommt.
Betrachten Sie zum Beispiel die Menge M, für die die folgende Definition gilt:
M := {3, 4, 5}
Es gelten die folgenden Elementbeziehungen:
- 3 ist Element von M. Formale Schreibweise: 3
 M.
M.
- 2 ist nicht Element von M. Formale Schreibweise: 2
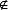 M.
M.
Eine weitere Menge P ist folgendermaßen definiert:
P := {x|x  5
5  x
x 
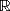 }
}
P ist also die Menge aller x, für die gilt: x ist kleiner als 5, und x ist Element der Menge der reellen Zahlen. Für diese Menge gelten die folgenden Elementbeziehungen:
4  P, aber 5
P, aber 5 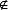 P
P
Beziehungen zwischen zwei Mengen
Eine Menge M heißt Teilmenge einer Menge N, wenn jedes Element von M auch Element von N ist, wenn also für jedes
x  M auch x
M auch x  N gilt.
N gilt.
Eine Menge M ist nicht Teilmenge einer Menge N, wenn es in M mindestens ein Element gibt, das nicht auch Element von
N ist. Es gibt also mindestens ein x  M, für das gilt: x
M, für das gilt: x 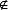 N.
N.
Betrachten Sie beispielsweise die folgenden Mengendefinitionen:
M := {3, 4, 5, 6}
N := {2, 4, 5, 6}
P := {3, 4, 5, 6, 7}
Es gelten die folgenden Mengenbeziehungen:
M 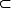 P (M ist Teilmenge von P)
P (M ist Teilmenge von P)
N 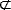 P (N ist nicht Teilmenge von P)
P (N ist nicht Teilmenge von P)
Übrigens ist die angegebene Teilmengendefinition ungenau: Die zuvor beschriebene Beziehung könnte ebenso gut bedeuten, dass zwei identische Mengen beschrieben werden. Deshalb heißt eine Menge M echte Teilmenge einer Menge N, wenn folgende Bedingungen gelten:
- Für jedes x
 M gilt auch x
M gilt auch x  N.
N.
- Es existiert mindestens ein x
 N, für das x
N, für das x 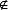 M gilt.
M gilt.
Wenn man es genau nimmt, wird nur für diese echte Teilmenge die Schreibweise
M 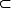 N verwendet. Für die weiter zuvor definierte allgemeine Teilmenge, bei der M = N
als Variante zulässig ist, wird stattdessen die Formulierung M
N verwendet. Für die weiter zuvor definierte allgemeine Teilmenge, bei der M = N
als Variante zulässig ist, wird stattdessen die Formulierung M 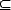 N (Teilmenge oder gleich) eingesetzt.
N (Teilmenge oder gleich) eingesetzt.
Wenn M 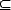 N gilt, wird N übrigens umgekehrt als Obermenge von M bezeichnet. Geschrieben wird dies als N
N gilt, wird N übrigens umgekehrt als Obermenge von M bezeichnet. Geschrieben wird dies als N 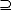 M (N ist Obermenge von oder gleich M). Die strengere Form M
M (N ist Obermenge von oder gleich M). Die strengere Form M 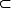 N (echte Teilmenge) bedeutet entsprechend, dass N echte Obermenge von M ist: N
N (echte Teilmenge) bedeutet entsprechend, dass N echte Obermenge von M ist: N  M.
M.
Eine Abfolge von Beziehungen echter Teilmengen beziehungsweise Obermengen lässt sich hervorragend an den Zahlenmengen der Mathematik demonstrieren. Dies sind im Einzelnen (von der speziellsten bis zur allgemeinsten) folgende:
- Die Menge der natürlichen Zahlen. Natürliche Zahlen sind alle Zahlen, mit denen sich Anzahlen ausdrücken lassen. Intuitiv
ist diese Menge folgendermaßen definiert:
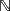 = {1, 2, 3, 4, ...}
= {1, 2, 3, 4, ...}
Die 0 gehört übrigens nicht zur Menge der natürlichen Zahlen, allerdings gibt es die spezielle Menge
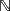 0, die zusätzlich die 0 enthält.
0, die zusätzlich die 0 enthält.
- Die Menge der ganzen Zahlen. Ebenso wie die natürlichen Zahlen sind auch die ganzen Zahlen intuitiv betrachtet
Zahlen ohne Nachkommastellen, allerdings mitsamt 0 und negativen Zahlen. Es handelt
sich um die folgende Menge:
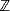 = {..., –3, –2, –1, 0, 1, 2, 3, ...}
= {..., –3, –2, –1, 0, 1, 2, 3, ...}
- Die Menge der rationalen Zahlen. Es handelt sich um sämtliche Zahlen, die durch die Division zweier ganzer Zahlen gebildet
werden können. Dies sind neben den ganzen Zahlen selbst alle abbrechenden und alle
periodischen Dezimalbrüche. Formal lautet die Definition dieser Menge folgendermaßen:
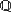 = {x | x = p/q
= {x | x = p/q  p
p 
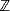
 q
q 
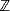
 q
q 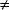 0}
0}
Bemerkenswert an dieser Menge ist, dass zwischen zwei rationalen Zahlen immer unendlich viele weitere rationale Zahlen liegen. Bei den natürlichen und ganzen Zahlen ist das anders: Da zwei Elemente dieser Mengen jeweils einen festgelegten numerischen Abstand (nämlich 1) voneinander haben, ist die Anzahl der Elemente zwischen zweien von ihnen jeweils endlich und steht fest.
- Die Menge der reellen Zahlen. Neben den abbrechenden und den periodischen Dezimalbrüchen gibt es auch unendlich
viele nichtabbrechende, nichtperiodische. Es handelt sich also um Zahlen mit unendlich
vielen Nachkommastellen ohne Wiederholung (Periode). Beispiele sind etwa die Kreiszahl
 (3,1415926...), die Eulersche Zahl e (2,718281828...) – die Basis des natürlichen
Logarithmus – oder
(3,1415926...), die Eulersche Zahl e (2,718281828...) – die Basis des natürlichen
Logarithmus – oder  2 (1,41421356...).
2 (1,41421356...).
Formal haben diese Zahlen miteinander gemeinsam, dass ihr Quadrat eine positive Zahl oder 0 ist:
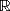 := {x | x2
:= {x | x2 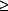 0}
0}
Beachten Sie, dass reelle Zahlen im Computer nicht dargestellt werden können, übrigens ebenso wenig wie periodische Dezimalbrüche. Wie im Folgenden ausgeführt, verwenden Rechner für jede Zahl eine festgelegte Anzahl von Bits und können Fließkommazahlen auf diese Weise mit einer bestimmten Genauigkeit, also nur mit einer endlichen Anzahl von Stellen, speichern.
- Die Menge der komplexen Zahlen. Eine Zahl mit negativem Quadrat ist intuitiv nicht vorstellbar (da sowohl positive
als auch negative Zahlen, wenn man sie mit sich selbst multipliziert, zu einem positiven
Ergebnis führen). Dennoch ist es zum Beispiel für mathematische Gedankenexperimente
oder bestimmte Berechnungen aus der theoretischen Physik erforderlich, die Wurzeln
negativer Zahlen zu berechnen.
Zu diesem Zweck werden die imaginären Zahlen eingeführt. Sie reduzieren das Problem der Wurzel aus negativen Zahlen auf die nicht reelle Komponente i, die als
 –1 definiert ist (und natürlich nicht durch eine normale Berechnung aufgelöst werden
kann). Jede imaginäre Zahl ist deshalb als Vielfaches von i definiert.
–1 definiert ist (und natürlich nicht durch eine normale Berechnung aufgelöst werden
kann). Jede imaginäre Zahl ist deshalb als Vielfaches von i definiert.
Die reellen und die imaginären Zahlen werden zusammengenommen als komplexe Zahlen (C) bezeichnet.
Jede der fünf hier genannten Mengen enthält die vorige. Die verkettete Beziehung von Teil- beziehungsweise Obermengen lautet also:
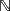
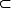
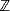
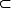
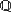
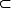
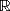
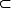
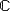
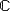

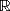

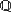

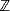

Verknüpfungen von Mengen
Ähnlich wie Sie einzelne Werte durch arithmetische Operatoren oder durch logische Verknüpfungen miteinander verbinden können, existieren spezielle Mengenoperationen, deren Ergebnis eine Verknüpfung der ursprünglichen Mengen ist.
- Die Schnittmenge. Die Schnittmenge M
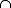 N zweier Mengen M und N enthält all diejenigen Elemente x, für die x
N zweier Mengen M und N enthält all diejenigen Elemente x, für die x  M und gleichzeitig x
M und gleichzeitig x  N gilt. Hier sehen Sie ein Beispiel:
N gilt. Hier sehen Sie ein Beispiel:
M := {1, 2, 3, 4}
N := {4, 5, 6, 7}
M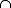 N = {4}
N = {4}
Beachten Sie, dass das Ergebnis nicht 4 lautet, sondern »die Menge, in der nur die 4 enthalten ist«. Eine Schnittmenge ist also auch dann eine Menge, wenn sie nur ein Element enthält. Wenn die beiden verknüpften Mengen keine gemeinsamen Elemente besitzen, geschieht sogar Folgendes:
M := {1, 2, 3}
N := {4, 5, 6}
M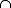 N = { } =
N = { } = 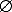
- Die Vereinigungsmenge. Die Vereinigungsmenge M
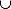 N zweier Mengen M und N ist die »verbundene« Menge aller x
N zweier Mengen M und N ist die »verbundene« Menge aller x  M und aller y
M und aller y  N. Hier ein Beispiel:
N. Hier ein Beispiel:
M := {1, 2, 3, 4}
N := {4, 5, 6, 7}
M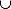 N = {1, 2, 3, 4, 5, 6, 7}
N = {1, 2, 3, 4, 5, 6, 7}
- Die Differenzmenge (Restmenge). Wenn aus der Menge M alle Elemente einer Menge N, die auch in M vorkommen, entfernt
werden, dann ist das Ergebnis die Differenzmenge M \ N, gesprochen »M ohne N«. Beispiel:
M := {1, 2, 3, 4}
N := {3, 4, 5}
M \ N = {1, 2}
2.1.5 Weitere wichtige Berechnungsverfahren
Bei der Implementierung von Computerprogrammen, aber auch bei der Lösung anderer Probleme des täglichen (Berufs-)Lebens sind einige weitere mathematische Verfahren wichtig. Dazu gehören unter anderem der Dreisatz und die Lösung von Gleichungssystemen. Zu diesen beiden Themen finden Sie hier je ein kurzes Beispiel mit Erläuterung.
Dreisatz
Der Dreisatz dient der Umrechnung von Verhältnissen: Wenn das Verhältnis zweier Werte zueinander bekannt und ein dritter Wert gegeben ist, kann daraus ein vierter Wert berechnet werden, der dasselbe Verhältnis zum dritten hat wie der zweite zum ersten. Mit anderen Worten wird in einer Gleichung wie der folgenden der Wert x gesucht:
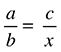
Um das Problem zu lösen, wird die Formel wie folgt nach x aufgelöst:
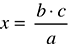
Hier ein konkretes Beispiel – wie die meisten Dreisatzprobleme als Textaufgabe formuliert und dem erweiterten IT-Umfeld entnommen: 25 m Netzwerkkabel von der Rolle kosten 13,95 €. Wie viel kosten 45 m?
Die ursprüngliche Formel lautet hier:
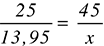
Nach x aufgelöst ergibt sich daraus:
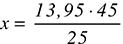
Dies kann nun leicht berechnet werden, und so erfährt man, dass 45 Meter Netzwerkkabel für 25,11 € zu haben sind – es sei denn, der Händler gewährt Mengenrabatt.
Lösen von Gleichungssystemen
Zuvor wurde bereits gezeigt, wie man eine einzelne Gleichung mit einer Unbekannten löst. Etwas schwieriger, aber keineswegs unmöglich ist es, Gleichungssysteme mit mehreren Unbekannten zu lösen. Dabei gilt als Faustregel, dass ein Gleichungssystem mit n Unbekannten nur dann eindeutig gelöst werden kann, wenn auch mindestens n Gleichungen vorhanden sind.
Die einfachste Lösungsmöglichkeit ist in der Regel das sogenannte Einsetzungsverfahren: Eine der Gleichungen wird nach einer Unbekannten aufgelöst; der Wert auf der anderen Seite des Gleichheitszeichens wird statt dieser Unbekannten in eine andere Gleichung eingesetzt. Auf diese Weise lässt sich die Anzahl der Unbekannten schrittweise reduzieren, bis sich eine Gleichung mit nur noch einer Unbekannten ergibt. Diese wird gelöst, und nun kann der konkrete Wert dieser Unbekannten zur Lösung der anderen Gleichungen verwendet werden.
Hier ein einfaches Beispiel, ein lineares Gleichungssystem mit zwei Unbekannten:
I x + y = 7
II 2x – y = 2
Zuerst wird eine der Gleichungen durch Umformungen nach einer der Unbekannten aufgelöst; hier die erste Gleichung nach y:
Ia x + y = 7 | –x
<=> y = 7 – x
Jetzt kann der Ausdruck 7–x statt y in die andere Gleichung eingesetzt werden; daraus wird dann durch erneutes Umformen der konkrete Wert von x berechnet:
Ia in II 2x – (7 – x) = 2
<=> 2x – 7 + x = 2
<=> 3x – 7 = 2 |+7
<=> 3x = 9 |:3
<=> x = 3
Da eine der Unbekannten nun einen konkreten Wert besitzt, kann dieser in eine der Gleichungen eingesetzt werden, um durch eine letzte Umformungsfolge auch den Wert der anderen Unbekannten zu erhalten:
x + y = 7
3 + y = 7 |–3
y = 4
Daraus ergibt sich die Lösungsmenge:
L = {3,4}
Komplexer als die bisher behandelten linearen Gleichungen und Gleichungssysteme sind die Gleichungen höheren Grades, bei denen die Unbekannte die Basis einer Potenz bildet; der Grad gibt dabei die höchste in der Gleichung vorkommende Potenz an.
Das einfachste Beispiel ist die quadratische Gleichung (Gleichung zweiten Grades), die folgende Normalform aufweist:
ax2 + bx + c = 0
Für solche Gleichungen existieren diverse Lösungsverfahren, deren Betrachtung hier allerdings zu weit führen würde.
Ihr Kommentar
Wie hat Ihnen das <openbook> gefallen? Wir freuen uns immer über Ihre freundlichen und kritischen Rückmeldungen.




 Jetzt bestellen
Jetzt bestellen






