2.4 Automatentheorien und -simulationen
Um die Funktionsweise von Computern nachvollziehen zu können, wurden im Lauf ihrer Entwicklungsgeschichte zahlreiche mathematisch-theoretische Modelle entworfen, die die grundlegenden Arbeitsschritte einer solchen Maschine verdeutlichen sollen. In diesem Abschnitt werden zwei der wichtigsten Theorien vorgestellt: der endliche Automat nach Turing sowie eine Modifikation einer Von-Neumann-Registermaschine (zu Letzterer siehe die Einleitung des nächsten Kapitels).
2.4.1 Algorithmen
Wie bereits in Kapitel 1, »Einführung«, erwähnt, verarbeitet ein Computer Abfolgen von Rechenvorschriften. Diese Vorschriften verarbeitet der Prozessor, indem er elektronische Schaltungen wie die im vorigen Abschnitt vorgestellten bedient. Automatentheorien beschreiben ausdrücklich nicht die elektrotechnischen Details von Computern, sondern die mathematischen Aspekte ihrer Funktionsweise. Gerade dies macht die Automatentheorien zum geeigneten Mittel, Algorithmen allgemeingültig zu formulieren, sodass sie auf vielen verschiedenen konkreten Rechnerarchitekturen realisiert werden können.
Algorithmen dienen in der Mathematik der Beschreibung von Rechen-, Konstruktions- oder Beweisverfahren. In der Informatik sind sie die allgemeine Grundlage für das Schreiben von Computerprogrammen. Umgekehrt dienen sie manchmal auch der Verallgemeinerung eines bestehenden Computerprogramms aus einer konkreten Programmiersprache auf eine allgemeinere Ebene, um das Programm zum Beispiel in einer anderen Sprache neu schreiben oder einige schlecht implementierte Teilfunktionen ersetzen zu können.
Neben einem Algorithmus wird in der Regel auch eine Datenstruktur benötigt. Datenstrukturen dienen der Speicherung der Informationen, die ein Algorithmus verarbeitet. Je nachdem, wie effizient eine Datenstruktur ist und wie gut sie an ein bestimmtes Problem angepasst ist, trägt sie entscheidend zu besseren oder schlechteren Algorithmen bei. Das Thema Algorithmen und Datenstrukturen wird in diesem Buch noch einmal aus der Sicht konkreter Programmiersprachen behandelt, und zwar im ersten Abschnitt von Kapitel 10, »Konzepte der Programmierung«.
Es gibt verschiedene konkrete Darstellungsformen für Algorithmen:
- Algebraische Darstellung: Die streng mathematisch-algebraische Darstellungsform beschreibt die Datenstruktur
als Algebra und die Rechenverfahren als Verknüpfungsvorschriften der Elemente dieser
Algebra.
Eine Algebra besteht aus einem Satz zulässiger Zeichen mit einer bestimmten Ordnung oder Abfolge sowie aus verschiedenen erlaubten Verknüpfungen dieser Zeichen. Zum Beispiel beschreibt die lineare Algebra sämtliche Aspekte linearer Gleichungssysteme, die Vektorrechnung und ihre Anwendungen wie etwa die euklidische Geometrie. Die Zeichen der linearen Algebra sind die reellen Zahlen beziehungsweise mehrdimensionale Vektoren aus reellen Zahlen. Die Verknüpfungsvorschriften sind die Grundrechenarten, die auf die Vektorrechnung ausgeweitet werden.
Ein anderes Beispiel ist die eingangs dargestellte boolesche Algebra, deren Zeichenvorrat aus 1 und 0 besteht; die wichtigsten zulässigen Verknüpfungen haben Sie ebenfalls bereits kennengelernt.
Für einen neu zu programmierenden Algorithmus eine eigene Algebra zu entwickeln ist eine schwierige Aufgabe und erfordert umfangreiche Kenntnisse der mathematischen Formelsprache. In diesem Buch wird aus konzeptionellen Gründen nicht weiter darauf eingegangen – es ist kein Mathematikbuch. In der Literaturliste in Anhang C finden Sie Hinweise auf Bücher, in denen diese Thematik näher erläutert wird.
- Anschaulich-sprachliche Darstellung: Überraschend häufig ist es am sinnvollsten, einen Algorithmus als Abfolge von Schritten in normaler Alltagssprache zu formulieren. Ein Beispiel sind die Umrechnungsanleitungen für die verschiedenen Zahlensysteme, die in diesem Kapitel bereits erläutert wurden. Der Ansatz, aus einer solchen Beschreibung ein Computerprogramm zu entwickeln, besteht darin, zunächst eine passende Datenstruktur auszuwählen und die einzelnen Schritte anschließend in Programmbefehle umzusetzen.
- Diagrammdarstellung: Eine beliebte Darstellungsform für Algorithmen ist das Flussdiagramm oder der konkretere, aus mehr Einzelschritten bestehende Programmablaufplan. In Kapitel 10, »Konzepte der Programmierung«, finden Sie Beispiele für einfache Flussdiagramme
nach DIN 66001. Ein anderes Verfahren, das vor allem im Informatikunterricht gern
eingesetzt wird, ist das Nassi-Shneiderman-Struktogramm; es bildet die Funktionen moderner Programmiersprachen
besser ab und lässt sich auf einfache Weise in Tabellenform darstellen.
Eine spezielle Variante der Diagrammdarstellung ist die Unified Modeling Language (UML). Sie dient nicht nur der Darstellung der unmittelbaren Computer-Algorithmen, sondern kann darüber hinaus ganze Geschäftsprozesse mitsamt beteiligten Ressourcen und Arbeitsabläufen abbilden. Auf diese Weise ist die UML eines der beliebtesten Instrumente im modernen Software-Engineering; sie dient dem objektorientierten Design und der Entwicklung verteilter Anwendungen. Genaueres erfahren Sie in Kapitel 11, »Software-Engineering«.
- Pseudocode-Darstellung: Es handelt sich um die Formulierung des Algorithmus in einer »verallgemeinerten Programmiersprache«. Diese Schreibweise kommt dem endgültigen Computerprogramm am nächsten, ist aber noch immer allgemein genug, um das Programm später in verschiedenen konkreten Sprachen implementieren zu können. Viele formalisierte Sprachen sind an Pascal oder BASIC angelehnt. Ein Beispiel auf einer anderen Ebene ist die Maschinensprache des in Abschnitt 2.4.3, »Der virtuelle Prozessor«, vorgestellten virtuellen Prozessors.
Berechenbarkeit und Komplexität
Die theoretische Informatik beschäftigt sich neben Automatentheorien vor allem mit den Problemen der Berechenbarkeit und der Komplexität.
Die Berechenbarkeit beantwortet die Frage, ob ein bestimmtes Problem überhaupt durch Berechnungen gelöst werden kann. Ein Teilproblem der Berechenbarkeit ist das Halteproblem, das sich mit der Frage beschäftigt, ob ein Algorithmus bei bestimmten Eingabewerten jemals terminiert (beendet wird). Manche Programme bleiben nämlich in einer Endlosschleife hängen, entweder aufgrund eines logischen Fehlers oder eben weil das gestellte Problem – zumindest für die eingegebenen Werte – gar nicht berechenbar ist.
Betrachten Sie als anschauliches Beispiel einen Algorithmus, der zwei Eingabewerte a und b entgegennimmt, a durch b dividiert und das Ergebnis ausgibt. Dargestellt werden könnte dieser Algorithmus etwa durch die folgende mathematische Funktion:
f (a,b) = a : b
Wie Ihnen bekannt sein dürfte, ist keine Zahl durch 0 teilbar, das heißt, für b = 0 ist die Funktion nicht berechenbar. Ein solcher Eingabewert heißt Undefiniertheitsstelle einer Funktion und wird so angegeben:
f (a,0) = 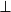
Intuitiv können Sie allerdings erkennen, dass die Funktion allgemein berechenbar ist
– es gibt unendlich viele Paare (a, b), für die sie eine definierte Lösung besitzt.
Genauer gesagt ist sie für alle a 
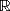 und alle b
und alle b 
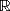 \{0} definiert.
\{0} definiert.
Es ist schwieriger, ein nicht berechenbares Problem zu finden, also eine Aufgabenstellung, die sich nicht durch Berechnung lösen lässt. Es gibt grundsätzlich zwei Kategorien nicht berechenbarer Probleme:
- Das Problem ist seiner Natur nach nicht berechenbar.
- Eine Berechnung zur Lösung des Problems ist so komplex, dass sie nicht in annehmbarer Zeit gelöst werden kann (die Berechnung würde mit vertretbarer Rechenkapazität viele Jahre oder gar Jahrhunderte dauern).
Beispiele für den ersten Fall enthalten meist einen unauflösbaren logischen Widerspruch. Der Klassiker in dieser Hinsicht ist die folgende Aussage:
Dieser Satz ist eine falsche Aussage.
Ein Prozessor würde eher durchschmoren, als Ihnen mit Gewissheit sagen zu können, ob diese Aussage wahr ist oder nicht. Falls sie nämlich tatsächlich wahr sein sollte, träfe es zu, dass sie falsch ist. Damit ist sie aber eben nicht wahr. Falls sie dagegen tatsächlich falsch ist, tritt das Gegenteil in Kraft, nämlich dass sie wahr ist ...
Die beliebte Geschichte vom Kreter, der behauptet, dass alle Kreter Lügner seien, ist dagegen kein echtes Paradoxon: Er muss ja lediglich selbst ein Lügner sein, und schon ist seine Aussage ohne jeden Widerspruch null und nichtig.
Einen viel zu hohen Aufwand stellt dagegen beispielsweise der Versuch dar, einen Algorithmus zu programmieren, der ein umfangreiches Kreuzworträtsel durch reines Ausprobieren löst oder sämtliche möglichen Züge bei einem Schachspiel durchprobiert. Letzteres scheint ein Widerspruch zu der Tatsache zu sein, dass es hervorragende Schachprogramme gibt, die sogar menschliche Weltmeister besiegen. Aber auch diese Programme versuchen gar nicht erst, jeden Zug durchzurechnen, sondern basieren auf einer Reihe von Wahrscheinlichkeitsregeln, Vereinfachungen und nicht zuletzt einer Datenbank mit sinnvollen Zügen.
Um die Rechenzeit zu bestimmen, die ein Algorithmus benötigt, wird dessen Komplexität ermittelt. Die Komplexitätsklasse gibt eine Größenordnung für die Anzahl der Durchläufe an, die bis zur Lösung des Problems zu tätigen sind. Für die tatsächliche Anzahl von Durchläufen werden drei exemplarische Werte angegeben: Der Best Case gibt die minimale Anzahl von Durchläufen an, der Average Case ist der Durchschnittswert und der Worst Case die maximale Durchlaufzahl.
Betrachten Sie als Beispiel einen Algorithmus, der die Elemente einer Menge nacheinander mit einem vorgegebenen Wert vergleicht und anhält, sobald ein Element diesem Wert entspricht oder alle Elemente verglichen wurden. Dieser Algorithmus wird als lineare Suche bezeichnet; in Kapitel 10, »Konzepte der Programmierung«, finden Sie eine Beispielimplementierung in einer echten Programmiersprache.
Der Best Case ist das Finden des Wertes beim ersten Versuch. Beim Worst Case müssen alle Elemente der Menge mit dem Suchwert verglichen werden. Der Average Case ist in diesem Fall die Hälfte der Elementanzahl. Die Komplexitätsklasse richtet sich grundsätzlich nach dem Worst Case, weil man bei der Programmierplanung berücksichtigen muss, wie lange die Ausführung eines Programms maximal dauern kann.
Der Algorithmus für die lineare Suche benötigt im Höchstfall eine Anzahl von Versuchen, die der Anzahl der Elemente entspricht. Bei n Elementen werden also maximal n Versuche gebraucht. Dies wird als lineare Komplexität (des Algorithmus) bezeichnet. Man sagt auch, dass die Komplexität »von der Ordnung n« ist.
Definition: Eine Funktion f(n) ist höchstens von der Ordnung der Funktion g(n), falls es eine Konstante C gibt, sodass für »große N« gilt:
f(N)  C·g(N)
C·g(N)
Dies wird symbolisch auch als f(N) = O(g(N)) geschrieben – die sogenannte O-Notation (Big-O-Notation).
Bei der linearen Suche ist g(N) = N, sodass für die Funktion f(N) gilt:
f(N) = O(N)
Übrigens spricht man auch dann von ein und derselben Komplexitätsklasse, wenn sich die Anzahl der Durchläufe zweier Algorithmen um einen konstanten Faktor voneinander unterscheidet. Benötigt ein anderer Algorithmus für n Elemente beispielsweise 2n Versuche, wird dies ebenfalls als lineare Komplexität angegeben.
Bei anderen Algorithmen kann es völlig andere Komplexitätsklassen geben. Stellen Sie sich beispielsweise ein Programm vor, das nacheinander alle erdenklichen Reihenfolgen einer Folge von n verschiedenen Werten ausgeben soll – dieses Verfahren wird als Suche nach Permutationen bezeichnet. Für die Zahlenfolge 1, 2, 3 gibt es beispielsweise die folgenden Permutationen:
|
1 |
2 |
3 |
|
1 |
3 |
2 |
|
2 |
1 |
3 |
|
2 |
3 |
1 |
|
3 |
1 |
2 |
|
3 |
2 |
1 |
Drei Elemente ermöglichen sechs verschiedene Permutationen, bei vier Elementen sind es bereits 24 (= 1 × 2 × 3 × 4). Bei n Elementen sind n! (sprich n Fakultät, also 1 × 2 × 3 × ...× n) verschiedene Permutationen möglich. Die Komplexitätsklasse ist demnach n!.
Andere typische Komplexitätsklassen sind etwa folgende:
- O(1) – statische Komplexität: Die Rechenzeit bleibt ungeachtet der Quantität N immer etwa gleich; dies ist ein Idealzustand, der selten erreicht wird. Der aktuelle Linux-Kernel 2.6 enthält einen O(1)-Scheduler. Es dauert also unabhängig von der Anzahl der laufenden Prozesse immer ungefähr gleich lang, auszuwählen, welcher als Nächster an der Reihe ist.
- O(log(N)) – die logarithmische Komplexität entsteht beispielsweise bei Teile-und-herrsche-Verfahren wie der in Kapitel 10, »Konzepte der Programmierung«, erläuterten binären Suche.
- O(N2) – quadratische Komplexität entsteht zum Beispiel bei Problemen, die die tabellarische Verknüpfung von Werten enthalten.
- O(NK) – die polynomielle Komplexität herrscht bei zahlreichen mehrdimensionalen Algorithmen.
- O(KN) – exponentielle Komplexität kommt bei Problemen vor, die durch mehrfaches Ausprobieren verschiedener Kombinationsmöglichkeiten gelöst werden.
2.4.2 Die Turing-Maschine
Eine der ältesten Automatentheorien wurde 1936, also noch vor der Verwirklichung echter Computer, von dem britischen Mathematiker, Kryptologen und Informatikpionier Alan Turing aufgestellt. Turing ist vor allem deshalb berühmt, weil er im Zweiten Weltkrieg die entscheidende Rolle bei der Entschlüsselung des Codes der deutschen Chiffriermaschine Enigma spielte.
Außerdem ist der von ihm erdachte Turing-Test bekannt. Dieses Konzept gilt als Maßstab dafür, wann ein Computer wirklich intelligent ist: Ein Mensch muss sich mit ihm über Monitor und Tastatur unterhalten können, ohne den Unterschied zu einer elektronischen Unterhaltung mit einem Menschen zu bemerken.
Einer der ersten Kandidaten für das Bestehen des Turing-Tests war übrigens das Programm Eliza, das in den 60er-Jahren von Joseph Weizenbaum geschrieben wurde. Es handelt sich um die Simulation eines Gesprächs zwischen einem Patienten und einem Psychotherapeuten, der die Eingaben des »Patienten« in Rückfragen umwandelt. Außerdem enthält das Programm eine Sammlung von Schlüsselwörtern, auf die es mit speziellen Antworten reagiert. Hier ein kurzer Beispieldialog:
User: I am afraid of computers.
Eliza: You have your mind on computers, it seems.
User: Yes.
Eliza: I see ... Well, why do you say this is so?
User: Because computers make me nervous.
Eliza: Is it because computers make you nervous that you came to me?
User: Yes.
Eliza: Yes, hmmm ... so, what makes you believe this is so?
User: Because I don’t trust them.
Eliza: Does it bother you that you do not trust them?
und so weiter
Mit Intelligenz hat das Ganze allerdings nichts zu tun; Eliza lässt sich leicht überlisten. Im Internet finden Sie zahlreiche Online-Implementierungen sowie Downloads für die verschiedensten Plattformen, oft mitsamt Quellcode, sodass Sie das Programm selbst analysieren können.
Übrigens kann man nicht über Alan Turing sprechen, ohne sein tragisches Schicksal zu erwähnen, zumal es ein beschämendes Beispiel dafür ist, wie weit Intoleranz getrieben werden kann: Als durch einen Zufall öffentlich bekannt wurde, dass Turing homosexuell ist, wurde er vom Gericht zu einer seltsamen Hormon-»Therapie« gezwungen. Dies zermürbte ihn letztlich so sehr, dass er sich 1954 das Leben nahm.[Anm.: Nach einigen Quellen behauptete Turings Mutter allerdings, dass es sich bei seiner Vergiftung ganz bestimmt um einen Unfall gehandelt habe. Plausibel wäre diese Variante deshalb, weil er sich trotz der entwürdigenden Behandlung bis zum letzten Tag seines Lebens voll in allerlei Forschungsprojekten engagierte.]
Eine der größten Leistungen Turings ist die Entwicklung des nach ihm benannten Automatenmodells, der Turing-Maschine. Eine allgemeinere Bezeichnung für solche Modelle ist endlicher Automat.
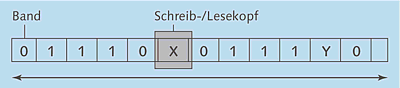
Eine Turing-Maschine besitzt den folgenden Aufbau:
- Der Speicher ist ein in einzelne Felder unterteiltes Band, das sich nach links oder rechts bewegen lässt. Aus diesem Grund wird die Turing-Maschine übrigens auch als Bandmaschine bezeichnet.
- Jedes Feld des Bandes kann einen bestimmten Wert aus dem Zeichenvorrat der Maschine enthalten.
- Es befindet sich jeweils genau ein Feld des Bandes unter einem Schreib-/Lesekopf. Dieser liest die Inhalte der einzelnen Felder zeichenweise als Eingabe oder schreibt als Ausgabe neue Werte hinein.
- Je nach gelesenem Zeichen und je nach bisherigem Zustand wird die Maschine in verschiedene
definierte Zustände versetzt. Die Zustände bestehen beispielsweise in der Bewegung des Bandes
in eine der beiden Richtungen, das Lesen des jeweils nächsten Zeichens, das Schreiben
eines Zeichens und so weiter. Ein spezielles Zeichen muss die Maschine jeweils in
den Zustand »Programmende« schalten.
Die Tatsache, dass es endlich viele verschiedene Zustände gibt, in denen sich eine solche Maschine befinden kann, begründet die Bezeichnung endlicher Automat.
Abbildung 2.15 zeigt den schematischen Aufbau einer Turing-Maschine. Beachten Sie, dass es neben der hier vorgestellten Ein-Band-Maschine auch Maschinen mit mehreren Bändern geben kann, die Aufgaben parallel erledigen können. Vorstellbar wäre etwa eine Turing-Maschine mit drei Bändern: Eingabeband, Rechenband und Ausgabeband.
Abbildung 2.15 Aufbau einer Turing-Maschine
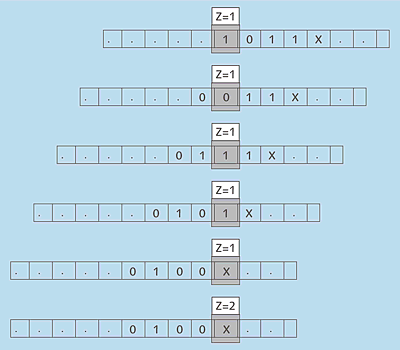
Das Prinzip lässt sich am besten anhand einer einfachen Maschine verdeutlichen, die einen kleinen Zeichenvorrat und wenige Zustände besitzt. Deshalb wird an dieser Stelle eine Turing-Maschine vorgestellt, die mit einem Alphabet aus drei Zeichen auskommt. Ihr Programm dient dazu, eine Dualzahl – bestehend aus den Symbolen 1 und 0 – bitweise zu invertieren, also aus jeder Null eine Eins zu machen und umgekehrt. Das Ende ist erreicht, wenn das spezielle Zeichen X angetroffen wird.
Das »Programm«, also die Definition der Zustandswechsel für diese Maschine, finden Sie in Tabelle 2.18. Jede Zelle in der Tabelle entspricht einer möglichen Kombination eines Zustands mit einem Wert, der zurzeit auf dem Band liegt. Jeder »Befehl« besteht aus dem neuen Wert, der geschrieben werden soll, aus dem neuen Zustand, in den gewechselt wird, sowie aus der Richtung, in die sich der Schreib-/Lesekopf auf dem Band weiterbewegen soll. Der Anfangszustand ist 1, der Zustand 2 steht dagegen für das Programmende.
| Zustand | 0 | 1 | X |
| 1 |
1;1;R |
0;1;R |
X;2;– |
| 2 |
Ende |
||
Wird im Zustand 1 eine 0 auf dem Band gelesen, dann wird eine 1 geschrieben, die Maschine verbleibt im Zustand 1 und wandert weiter nach rechts (R). Bei einer 1 wird der Wert 0 geschrieben, abgesehen davon geschieht dasselbe. Wenn ein X gelesen wird, wechselt die Maschine in den Zustand 2, in dem die Berechnung beendet ist.
Angenommen, das Band enthält die Werte 1011X: Die Maschine führt somit nacheinander die in Abbildung 2.16 gezeigten Arbeitsschritte durch.
Eine Maschine mit einem etwas größeren Zeichenvorrat – hinzu kommt ein Y – soll nun eine andere Aufgabe ausführen: Die einzelnen gelesenen Werte, die sich anfangs links vom X befinden, sollen hinter das X gestellt werden, und zwar in umgekehrter Reihenfolge. Dazu bewegt die Maschine den Schreib-/Lesekopf zunächst immer weiter nach rechts, bis sie beim X ankommt. Rechts vom X trägt sie ein Y als Stoppmarkierung ein. Hier geht sie einen Schritt zurück, um den am weitesten rechts stehenden Wert zu holen. Je nachdem, welcher Wert das ist, gibt es zwei verschiedene Zustände, die den Wert beide mit einem X überschreiben und dann immer weiter nach rechts wandern, bis das Y gelesen wird. Dort legen sie den Wert (1 oder 0) ab, für den sie zuständig sind, und notieren das Y dahinter. Anschließend geht das Ganze von vorn los.
Tabelle 2.19 zeigt die Programmvorschriften, die zur Lösung dieses Problems erforderlich sind. Das »fünfte Zeichen« mit der symbolischen Beschriftung ».« steht für eine leere Zelle auf dem Band.
Abbildung 2.16 Arbeitsablauf eines einfachen Turing-Maschinenprogramms
Auf der Website zum Buch finden Sie Links zu einigen Turing-Maschinensimulationen, in denen Sie die hier dargestellten Beispiele und andere Programme ausprobieren können.
Turing-Maschinen sind in der Lage, jedes beliebige berechenbare Problem zu lösen. Deshalb ist ein wichtiges Kriterium für die Funktionalität einer Programmiersprache die Frage, ob sie Turing-vollständig ist, das heißt alle Probleme lösen kann, mit denen auch die Turing-Maschine zurechtkommt.
2.4.3 Der virtuelle Prozessor
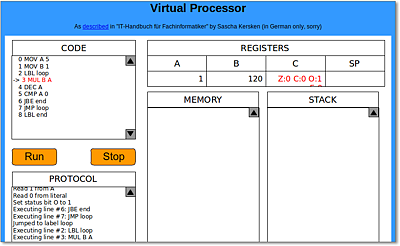
Eine andere Art der Computersimulation ist die Registermaschine, die das Modell des Von-Neumann-Rechners simuliert. In diesem Abschnitt wird sie durch einen einfachen virtuellen Prozessor dargestellt. Es handelt sich um die stark vereinfachte Simulation eines Mikroprozessors. Er kann einige, aber bei Weitem nicht alle Operationen durchführen, die ein echter Prozessor auch ausführen kann. Allerdings ließe sich mit etwas Mühe nachweisen, dass er Turing-vollständig ist, also alle berechenbaren Probleme lösen kann.
Abbildung 2.17 Die Flash-Simulation des virtuellen Prozessors berechnet die Fakultät von 5.
Auf der Website zum Buch finden Sie unter der Adresse http://buecher.lingoworld.de/fachinfo/vprocessor.html eine Flash-Simulation dieses Prozessors. In Abbildung 2.17 sehen Sie diese Simulation bei der Ausführung eines Programms, das die Fakultät von 5 berechnet. Alternativ können Sie die Arbeit dieses Prozessors auch mit Bleistift und Papier nachvollziehen.
In der sehr einfachen »Maschinensprache« des virtuellen Prozessors wird ein Programm geschrieben, das dann – in der Papierversion von Ihnen, in der Computersimulation durch den Rechner – ausgeführt wird.
Es gelten die folgenden Designprinzipien für den Prozessor und den umgebenden Computer (der nur durch seinen Arbeitsspeicher vertreten ist):
- Der Prozessor besitzt nur zwei Rechenregister A und B sowie ein Statusregister C und einen Stack Pointer S.
- Der adressierbare Arbeitsspeicher besitzt die Adressen 0–199. Das Programm als solches
wird nicht als Bestandteil des Arbeitsspeichers gehandhabt (bei echten Prozessoren
kann es zu Abstürzen kommen, wenn versehentlich oder absichtlich der Programmspeicher
überschrieben wird). Programmstellen werden nicht durch Speicheradressen, sondern
durch spezielle Sprungmarken (Labels) angegeben.
Die Speicherstellen 100 bis 199 bilden übrigens den sogenannten Stack, der im Rahmen der Befehlsreferenz erläutert wird, und sollten deshalb nicht als normale Einzelspeicherstellen verwendet werden.
- Der Prozessor behandelt Ganzzahlen und Fließkommazahlen gleich und macht keine Unterschiede zwischen ihnen. Soll ein Speicherbereich als Adresse interpretiert werden (indirekte Adressierung), so wird nur der ganzzahlige Anteil vor dem Komma betrachtet.
- Es gibt im Speicher keine maximale Wortlänge, er ist also nicht in Einheiten wie Bytes
oder 32-Bit-Blöcke eingeteilt. Eine Speicherstelle kann eine beliebig große Zahl aufnehmen.
Eine Einschränkung ergibt sich natürlich bei der Simulation auf einem echten Computer: Hier entspricht die maximale Aufnahmekapazität einer Speicherstelle der jeweiligen Computerarchitektur. Typischerweise können zum Beispiel 32 Bit für Ganzzahlen gespeichert werden, es sind also Werte zwischen etwa –2 Milliarden und +2 Milliarden möglich.
- Eine Ebene der echten Maschinensprache, auf der jeder Befehl einer Zahl (OpCode) entspricht, wurde gar nicht erst realisiert. Die unterste Ebene ist der »Assembler« des virtuellen Prozessors, der die Befehle als benannte Kürzel – sogenannte Mnemonics – abbildet. Soweit es bei einer so einfachen CPU möglich ist, wurden die Namen und Funktionen der Befehle dem Intel-Assembler angepasst.
Zum Einstieg sehen Sie hier als Erstes ein Programmbeispiel. Die Nummern in Klammern beziehen sich auf die anschließenden Erläuterungen:
MOV A, $0 ;(1)
ADD A, $1 ;(2)
MOV $2, A ;(3)
HLT ;(4)
Hier die Erläuterung des Programms:
- MOV A, $0. Der Inhalt der Speicheradresse 0 wird in das Rechenregister A kopiert.
- ADD A, $1. Der Inhalt von Adresse 1 wird zum Inhalt von Register A addiert.
- MOV $2, A. Der Inhalt des Registers A wird in die Speicherstelle 2 kopiert.
- HLT. Das Programm wird beendet.
Um die Simulation durchführen zu können, werden die Speicheradressen 0 und 1 mit den Anfangswerten 3 und 4 belegt. Die Ausführung des Programms kann wie folgt in einer Wertetabelle dargestellt werden.
| Befehl | A | 0 | 1 | 2 |
|
– |
– |
3 |
4 |
– |
|
MOV A,$0 |
3 |
3 |
4 |
– |
|
ADD A,$1 |
7 |
3 |
4 |
– |
|
MOV $2, A |
7 |
3 |
4 |
7 |
Befehlsreferenz
In der folgenden Referenz werden einige wichtige Abkürzungen verwendet:
- reg ist ein Rechenregister (A oder B).
- addr ist eine Datenspeicheradresse (0 bis 199).
- val steht für einen beliebigen numerischen Wert.
- lbl gibt eine Sprungmarke an.
Einer der wichtigsten Befehle ist MOV. Die Bezeichnung ist eigentlich unglücklich gewählt, da der fragliche Wert nicht an eine andere Stelle verschoben, sondern dorthin kopiert wird. Die allgemeine Schreibweise ist MOV ziel, quelle und bedeutet, dass ein Wert von quelle nach ziel kopiert werden soll. Im Einzelnen existieren die folgenden Varianten des MOV-Befehls:
- MOV reg, reg – kopiert den Inhalt eines Registers in das andere. Beispiel: MOV A, B legt den Inhalt des Rechenregisters B auch im Register A ab.
- MOV reg, $addr – dieser Befehl kopiert den Inhalt der angegebenen Adresse addr in das Register reg. Das Dollarzeichen dient der Unterscheidung zwischen einer Speicheradresse und einem konstanten Wert. Beispiel: MOV A, $4 legt den Inhalt der Speicheradresse 4 im Register A ab.
- MOV reg, val – kopiert den konstanten Wert val in das Register reg. Beispiel: MOV B, 7 speichert den Wert 7 im Rechenregister B.
- MOV $addr, reg – der Inhalt des Registers reg wird in die Adresse addr kopiert. Beispiel: MOV $9, A – der Inhalt von A wird in die Speicheradresse 9 kopiert.
- MOV $addr, $addr – der Befehl kopiert den Inhalt einer Adresse in eine andere Adresse. Beispiel: MOV $10, $11 – der Wert aus der Speicheradresse 11 wird in Adresse 10 kopiert.
- MOV $addr, val – kopiert den konstanten Wert val in die Adresse addr. Beispiel: MOV $99, 22 kopiert den Wert 22 in die Adresse 99.
Die folgenden Rechenbefehle funktionieren mit denselben Optionen:
- ADD ziel, quelle – der Inhalt von quelle wird zu ziel addiert.
- SUB ziel, quelle – der Inhalt von quelle wird von ziel abgezogen.
- MUL ziel, quelle – ziel wird mit dem Inhalt von quelle multipliziert.
- DIV ziel, quelle – ziel wird durch den Inhalt von quelle dividiert. Ist der Inhalt von quelle 0, bleibt der Wert von ziel erhalten, und das ERROR-Flag E des Statusregisters wird auf 1 gesetzt.
Die beiden folgenden speziellen Rechenbefehle funktionieren nur mit einem Register oder einer Adresse als Ziel.
- INC ziel (»increment«) erhöht den Wert von ziel um 1.
- DEC ziel (»decrement«) vermindert den Wert von ziel um 1.
Die nächste Kategorie von Befehlen sind die Vergleichsoperationen. Sie alle verändern die Flags im Statusregister C. Dieses Register ist folgendermaßen aufgebaut:
|
Z |
C |
O |
E |
- Jedes der vier Flags Z (»zero«), C (»carry«), O (»overflow«) und E (»error«) ist 1 Bit groß und kann demzufolge einen der Werte 1 oder 0 annehmen.
Wie bei echten Prozessoren wird der eigentliche Vergleich als Subtraktion ausgeführt und verändert die Werte der Flags entsprechend: Bei Vergleichsoperationen wird das Zero-Flag auf 1 gesetzt, wenn die beiden Werte gleich sind (Ergebnis 0), das Carry-Flag auf 1, wenn der erste Operand kleiner als der zweite ist, und das Overflow-Flag auf 1, wenn der zweite Operand größer ist. Die beiden jeweils anderen Vergleichs-Flags werden auf 0 gesetzt. Das Overflow-Flag zeigt außer seiner Aufgabe bei Vergleichen einen Stack Overflow an.
Bei echten Prozessoren bedeutet Carry übrigens »Übertrag«; dieses Flag hat dort also die Aufgabe, anzuzeigen, dass das Ergebnis einer Operation nicht mehr in den ursprünglichen Speicherplatz der Operanden hineinpasst. Bei diesem virtuellen Prozessor kann das nicht passieren, da es keine maximale Wortbreite gibt.
Der Vergleich zweier Werte wird durch den folgenden Befehl durchgeführt: CMP operand1, operand2. Die beiden Operanden können alle möglichen Kombinationen sein, die auch für Rechenoperationen gelten. Zusätzlich können Sie hier zwei konstante Werte miteinander vergleichen, da nirgendwo ein Rechenergebnis abgelegt werden muss.
Hinter dem Vergleichsbefehl, der die Flags in einen bestimmten Zustand versetzt, steht meist unmittelbar ein Sprungbefehl. Zu unterscheiden ist zwischen bedingten und unbedingten Sprüngen:
- Unbedingte Sprünge finden auf jeden Fall statt.
- Bedingte Sprünge finden nur dann statt, wenn die Flags aufgrund eines Vergleichs oder eines Fehlers bestimmte Werte besitzen.
Wichtig ist in diesem Zusammenhang der Befehl zum Setzen einer Sprungmarke: LBL lbl definiert eine Stelle im Programmspeicher, die Ziel eines Sprungs sein kann. lbl ist eine beliebige Kombination aus Buchstaben und Ziffern; das erste Zeichen muss ein Buchstabe sein. Es wird nicht auf Groß- und Kleinschreibung geachtet.
Die folgenden Sprungbefehle sind definiert:
- JMP lbl – der Befehl führt einen unbedingten Sprung zu der Stelle durch, die durch das Label lbl bezeichnet wird.
- JA label – der Befehl steht für »jump if above« und springt zu lbl, wenn beim davor ausgeführten Vergleich der erste Operand größer als der zweite war (O-Flag auf 1).
- JAE lbl – der Befehl »jump if above or equals« springt zu lbl, wenn der erste Operand größer oder gleich dem zweiten war, wenn also das O-Flag oder das Z-Flag auf 1 steht.
- JB lbl – der Befehl »jump if below« springt zu lbl, wenn der erste Operand kleiner als der zweite war (C-Flag auf 1).
- JBE lbl – der Befehl »jump if below or equals« springt zu lbl, wenn der erste Operand kleiner oder gleich dem zweiten war (C-Flag auf 1 oder Z-Flag auf 1).
- JE lbl – der Befehl »jump if equals« springt zu lbl, wenn die beiden Operanden gleich waren (Z-Flag auf 1).
- JNE lbl – der Befehl »jump if not equals« springt zu lbl, wenn die beiden Operanden unterschiedlich waren (C-Flag auf 1 oder O-Flag auf 1).
- JR lbl – der Befehl »jump if error« springt zu lbl, wenn zuvor ein Fehler aufgetreten ist (E-Flag auf 1). Wird der Fehler (zum Beispiel die Division durch 0) nicht unmittelbar nach der fraglichen Operation auf diese Weise abgefangen, kommt es zum automatischen Programmhalt.
- JO lbl – der Befehl »jump if overflow« ist im Prinzip synonym zu JA, wird aber verwendet, um Stack Overflows nach PUSH-Befehlen abzufangen.
Die Stack-Befehle dienen der Arbeit mit einem speziellen Speicherbereich, dem Stack (Stapel), um Werte nacheinander daraufzulegen und wieder herunterzunehmen. Der Stack-Befehl arbeitet nach dem LIFO-Prinzip, also »Last In, First Out«. Schematisch ist der Stack bei diesem virtuellen Prozessor genauso organisiert wie bei echten Computerarchitekturen: Ab der Speicherstelle 199 wächst der Stack nach unten. Das spezielle Register S (Stack Pointer) zeigt den obersten (also in Wirklichkeit untersten) Speicherplatz an, der zurzeit vom Stack belegt wird.
Beachten Sie, dass der Stack bei diesem virtuellen Prozessor lediglich für die Lösung von Programmieraufgaben verwendet wird. Einige solcher Probleme werden in Kapitel 10, »Konzepte der Programmierung«, näher erläutert. Bei einem echten Prozessor besitzt der Stack zusätzlich die Aufgabe, Rücksprungadressen für Unterprogramme aufzunehmen – siehe Kapitel 3, »Hardware«.
Der Stack kann mithilfe der beiden folgenden Operationen bedient werden:
- PUSH quelle – der Inhalt von quelle wird oben auf den Stack gelegt. quelle kann wie üblich reg, $addr oder val sein. Ist der Stack voll (er fasst maximal 100 Werte), wird das O-Flag gesetzt. Deshalb sollte nach PUSH-Befehlen aus Sicherheitsgründen stets ein JO-Befehl stehen.
- POP ziel – der oberste Wert wird vom Stack genommen und in ziel abgelegt; dieses Ziel kann reg oder $addr sein. Ist der Stack leer, bleibt der Inhalt von ziel unverändert, und das E-Flag wird gesetzt. Sinnvollerweise sollte also direkt nach jeder POP-Operation ein JR-Befehl stehen.
Zu guter Letzt bedeutet der Befehl HLT (ohne Argumente), dass das Programm gestoppt werden soll. Beim letzten Befehl hält es übrigens von selbst an. HLT ist vor allem dazu gedacht, es an einer bestimmten Stelle zu beenden, an der noch Befehle folgen.
Zwei Beispiele
Zum Schluss finden Sie hier noch zwei Beispielprogramme, die auf dem virtuellen Prozessor ausgeführt werden können. Wenn Sie selbst ein gutes Programm für den virtuellen Prozessor schreiben, können Sie mir dieses gern per E-Mail, über die Facebook-Seite zum Buch oder über das Feedback-Formular auf meiner Website zukommen lassen. Die schönsten Beispiele veröffentliche ich gern mit Autorenangaben auf der Site.
Beachten Sie, dass ein Semikolon in einer Zeile einen Kommentar einleitet – auch bei der Computersimulation des virtuellen Prozessors können Sie Erläuterungen dahinterschreiben.
Das erste Beispiel addiert sämtliche Werte, die auf dem Stack liegen, in der Speicherstelle 3:
MOV $3, 0 ; Speicherstelle 3 zurücksetzen
LBL start ; Sprungmarke setzen
POP B ; Wert vom Stack in B
JR ende ; Ende, wenn Stack leer
ADD $3, B ; Inhalt von B zu $3 addieren
JMP start ; Schleife: nächsten Wert verarbeiten
LBL ende
HLT
Falls Sie das Programm auf dem Papier ausprobieren möchten, können Sie den Stack einfach mit einigen Beispielwerten belegen und sich anschließend eine Wertetabelle zeichnen. In der Flash-Simulation können Sie ein paar PUSH-Befehle vor das hier abgedruckte Programm setzen, um Werte auf den Stack zu legen. Anschließend können Sie das Programm laufen lassen und beobachten, was passiert.
Das zweite Beispiel löst die in Kapitel 1, »Einführung«, erwähnte Aufgabe, die Onlinekosten eines Internetnutzers zu berechnen. Der Provider bietet zwei Tarife an: Im Tarif 1, der Flatrate, zahlt der Kunde pauschal 29,99 €. Der Tarif 2 ist zeitbasiert; es gibt eine Grundgebühr von 2,49 € und einen Minutenpreis von 0,01 €. In Speicherstelle 10 steht der Tarif (1 oder 2); Adresse 11 enthält die Minuten, die der Kunde online verbracht hat. Das Ergebnis der Berechnung wird in Adresse 20 geschrieben.
MOV A, $10 ; Tarif in Register A
CMP A, 1 ; Ist es Tarif 1?
JE flat ; - dann zum Label flat springen
MOV B, $11 ; Minuten in Register B
MUL B, 0.01 ; B mit dem Minutenpreis multiplizieren
ADD B, 5 ; Grundgebühr addieren
MOV $20, B ; Ergebnis in Adresse 20
HLT
LBL flat ; Hier Flatrate-Berechnung
MOV $20, 19.99 ; Pauschalpreis in Adresse 20
HLT
Die Flash-Simulation meldet manchmal »Invalid Mnemonic in <Zeile>«, wobei <Zeile>
der ab 0 gezählten letzten Zeile entspricht – vor allem, wenn Sie ein Programm aus
der Zwischenablage einfügen. Das liegt daran, dass das Programm in der gegenwärtigen
Fassung keine leeren Zeilen enthalten darf und sich am Ende ein Zeilenumbruch befindet.
Klicken Sie in diesem Fall einfach mit der Maus in die Zeile unter dem Code, und betätigen
Sie die  -Taste.
-Taste.
Ihr Kommentar
Wie hat Ihnen das <openbook> gefallen? Wir freuen uns immer über Ihre freundlichen und kritischen Rückmeldungen.




 Jetzt bestellen
Jetzt bestellen






